题目描述

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。

请你找出这两个正序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2不会同时为空。

样例

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

算法分析

给定两个有序的数组，找中位数(n + m) / 2，等价于找第k小的元素，k = (n + m) / 2

• 1、当一共有偶数个数时，找到第total / 2小left和第total / 2 + 1小right，结果是(left + right / 2.0)
• 2、当一共有奇数个数时，找到第total / 2 + 1小，即为结果

如何找第k小？

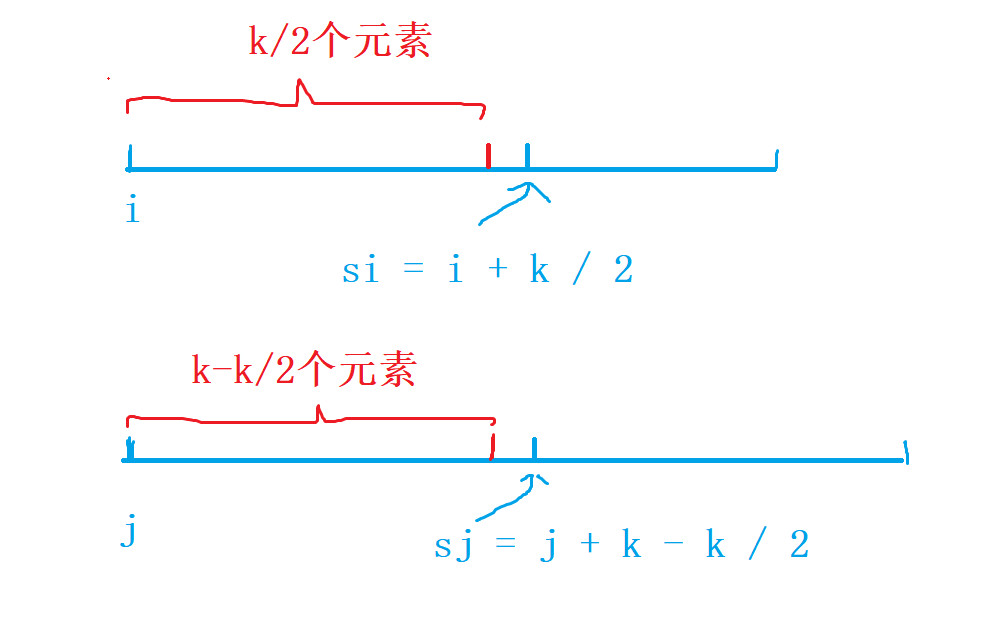
• 1、默认第一个数组比第二个数组的有效长度小
• 2、第一个数组的有效长度从i开始，第二个数组的有效长度从j开始，其中[i,si - 1]是第一个数组的前k / 2个元素，[j, sj - 1]是第二个数组的前k - k / 2个元素
• 3、当nums1[si - 1] > nums2[sj - 1]时，则表示第k小一定在[i,n]与[sj,m]中
• 4、当nums1[si - 1] <= nums2[sj - 1]时，则表示第k小一定在[si,n]与[j,m]中

时间复杂度 $Olog(n + m)$

Java 代码

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int total = nums1.length + nums2.length;
        if(total % 2 == 0)
        {
            int left = f(nums1,0,nums2,0,total / 2);
            int right = f(nums1,0,nums2,0,total / 2 + 1);
            return (left + right) / 2.0;
        }
        else return f(nums1,0,nums2,0,total / 2 + 1);
    }
    static int f(int[] nums1,int i,int[] nums2,int j,int k)
    {
        //默认第一个是小的
        if(nums1.length - i > nums2.length - j) return f(nums2,j,nums1,i,k);
        //当第一个数组已经用完
        if(nums1.length == i) return nums2[j + k - 1];
        //当取第1个元素
        if(k == 1) return Math.min(nums1[i],nums2[j]);

        int si = Math.min(nums1.length,i + k / 2),sj = j + k - k / 2;
        if(nums1[si - 1] > nums2[sj - 1])
        {
            return f(nums1,i,nums2,sj,k - (sj - j));
        }
        else
        {
            return f(nums1,si,nums2,j,k - (si - i));
        }
    }
}