算法思路

dfs + 回溯解题框架

dfs算法的过程其实就是一棵递归树，所有的dfs算法的步骤大概有以下几步：

• 找到中止条件，即递归树从根节点走到叶子节点时的返回条件，此时一般情况下已经遍历完了从根节点到叶子结点的一条路径，往往就是我们需要存下来的一种合法方案
• 如果还没有走到底，那么我们需要对当前层的所有可能选择方案进行枚举，加入路径中，然后走向下一层
• 在枚举过程中，有些情况下需要对不可能走到底的情况进行预判，如果已经知道这条路不可能到达我们想去的地方，那我们干嘛还要一条路走到黑呢，这就是我们常说的剪枝的过程
• 当完成往下层的递归后，我们需要将当前层的选择状态进行清零，它下去之前是什么样子，我们现在就要让它恢复原状，也叫恢复现场。该过程就是回溯，目的是回到最初选择路口的起点，好再试试其他的路。

将上面的算法框架应用于对于本题，根据习惯，枚举时我们可以选择每个位置放哪个数，同时也可以枚举每个数放在哪个位置。 不同枚举顺序，就会画出不同的递归搜索树（如下图），接下来我们就分别分析以下两种情况：

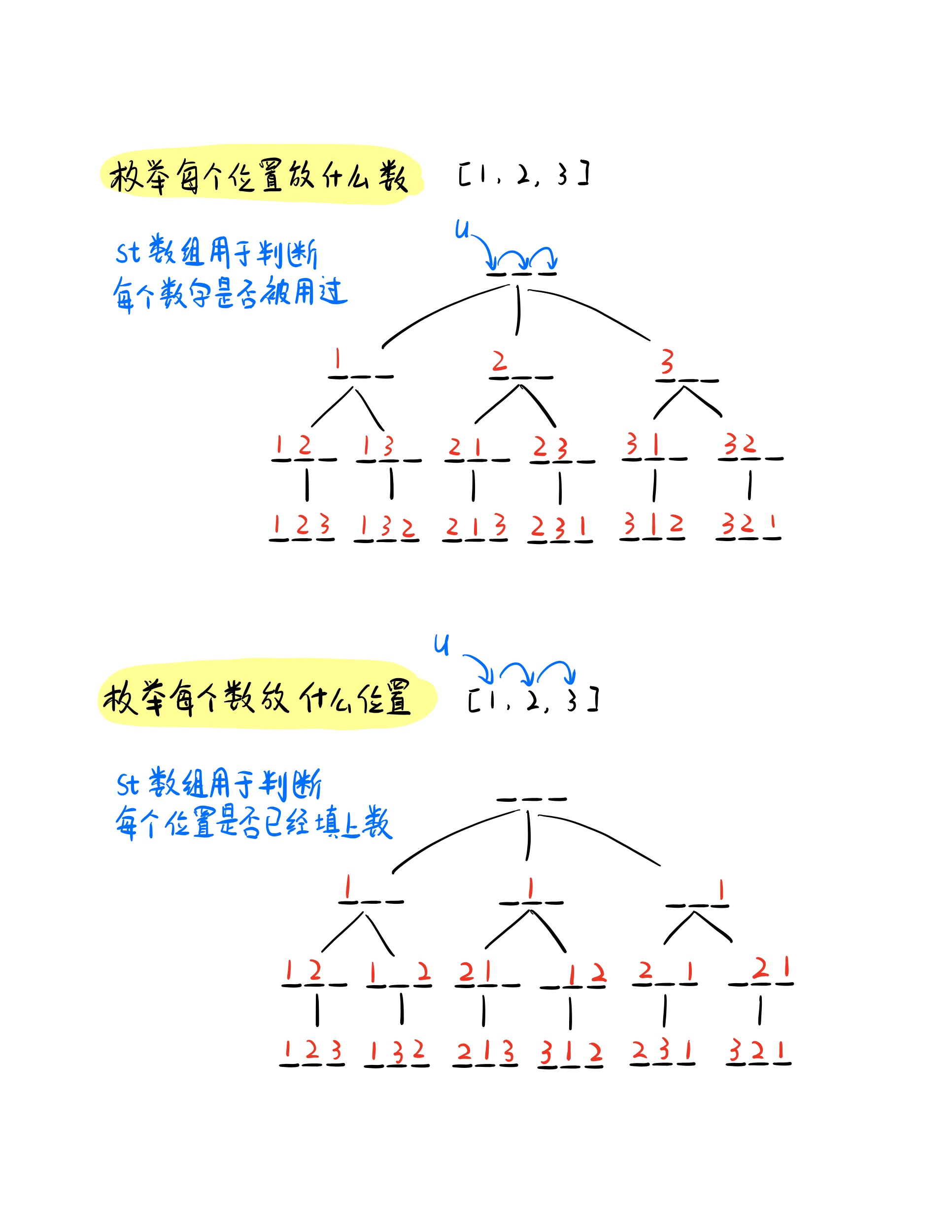
枚举每个位置放什么数

1. 因为我们需要枚举每个位置放什么数，因此当我们每个位置都放好数，我们就走到了递归树的叶子节点，此时将我们的该路径加入方案中。

2. 如果还没有到达叶子结点，那么我们需要枚举选择该位置放哪些数，因为我们每个数都必须用且只能用一次，所以我们利用st数组来标记那些数被用过。枚举每一个数，如果没有用过，即可加入路径并标记，然后递归到下一层，即下一个位置。

3. 递归结束后，我们需要恢复现场，消除刚才的标记，并把刚才放在该位置上的数清空，即弹出。这样做的目的是因为当前位置上还可以选择放其他数，所以需要回到往下走之前的样子，然后再选择其他路。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permute(vector<int>& nums) {
        st = vector<bool> (nums.size());
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到了方案数组path的哪个位置
    {
        if (u == nums.size()) //遍历完整个数组
        {
            res.push_back(path); //加入方案
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举当前位置可以选择哪些数
        {
            if (!st[i]) //没有选过
            {
                path.push_back(nums[i]); //选择该数
                st[i] = true; //标记选过
                dfs(nums, u + 1); //继续递归下一层
                st[i] = false; //回溯
                path.pop_back(); //回溯
            }

        }
    }
};

枚举每个数放哪个位置

1. 因为我们需要枚举每个数放什么位置，因此把所有数都放到了位置上，我们就走到了递归树的叶子节点，此时将我们的该路径加入方案中。

2. 如果还没有到达叶子结点，那么我们需要枚举当前数可以放在哪个位置，显然每个位置只能放一个数，所以我们利用st数组来标记那些位置上已经放好数了。枚举每个位置，如果没有放上任何数，即可在该位置放上数，然后递归到下一层，即继续去放下一个数。

3. 递归结束后，我们需要恢复现场，消除刚才的标记，由于只要当前位置的标记被清空，该位置就可以放数，所以当我们放下一个数时，如果发现该位置没有用过，即可放上去，此时刚好就能覆盖本来填上的数，因此位置上的数并没有必要清空。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permute(vector<int>& nums) {
        path = vector<int> (nums.size());
        st = vector<bool> (nums.size());
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到了数组中的哪个数
    {
        if (u == nums.size()) //遍历完整个数组
        {
            res.push_back(path); //加入方案
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举每个位置
        {
            if (!st[i]) //如果该位置还没有放任何数
            {
                path[i] = nums[u]; //
                st[i] = true;
                dfs(nums, u + 1);
                st[i] = false;
            }
        }
    }
};