算法思路

DFS + 回溯

阅读此篇之前建议先阅读LeetCode 46. 全排列 ，与上一题不同的是，该题目给的数组里面可能出现相同元素。如果根据我们上题的做法，我们可以选择每个数可以放在哪些位置，同时我们也可以选择每个位置放哪些数，然后画出以下递归搜索树。

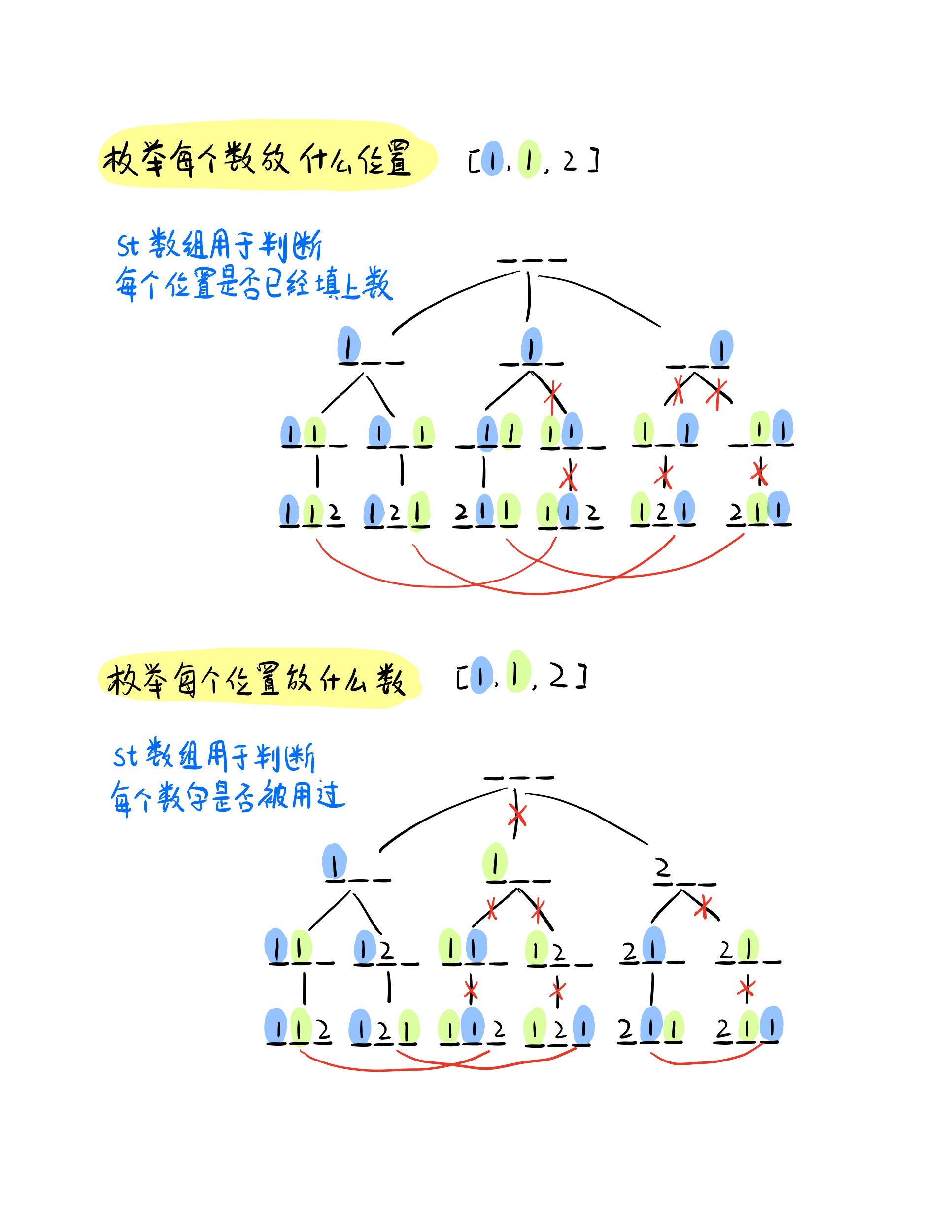
枚举每个数可以放在什么位置

如果把两个1当作不同的数，所有的方案就是下图中的叶子节点，但是很不幸，由于相同元素的出现，我们的最终方案也出现了重复。找到重复的情况，通过不同颜色的标记可以看出，对于相同的两个位置，蓝色的1在前或者绿色的1在前，方案只需要计算其中一个。因此我们可以人为地规定绿色的1只能出现在蓝色的1的后面，这样我们就可以避免重复方案了。

为了实现上述过程，我们需要将原数组中的元素进行排序，然后将原数组中元素之间的相对位置作为每一种方案中元素的相对位置。所以我们需要传入参数时添加一个参数start，该参数的意义是在枚举该数可以放哪些位置时，位置的枚举需要从start开始。这样当我们需要递归到下一层时，如果下一个选择的数和当前的数相等，因为在原数组中下一个数在当前数的后面，因此在放下一个数时也必须放在当前数的后面，因此传入参数start等于当前数所填位置的下一个位置。如果下一个数不同，那么就没有限制，位置枚举从0开始。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        path = vector<int> (n);
        st = vector<bool> (n);
        dfs(nums, 0, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u, int start)
    {
        if (u == nums.size())
        {
            res.push_back(path);
            return;
        }

        for (int i = start; i < nums.size(); i ++) //枚举哪个位置可以放该数
        {
            if (!st[i]) //没有放数
            {
                path[i] = nums[u];
                st[i] = true;
                dfs(nums, u + 1, u + 1 < nums.size() && nums[u + 1] == nums[u] ? i + 1 : 0);
                //下一个数和当前摆放的数不同，可以选择任意位置；如果相同，必须摆放在该数后面
                st[i] = false; //回溯
            }
        }
    }
};

枚举每个位置可以放哪些数

以该种枚举顺序，我们可得下图递归搜索树，我们可以看出，出现重复方案的原因是因为，当我们在枚举某一位置时，如果我们将两个1看作是不同元素，那么我们枚举时可以选择把哪个1放在该位置上.但是明显放蓝色的1和绿色的1最终的方案都是一样的，因此我们在枚举每个位置可以放哪些数时，如果下一个选择的数和当前选择的数相同，那么我们就跳过。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        path = vector<int> (n);
        st = vector<bool> (n);
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到的位置
    {
        if (u == nums.size())
        {
            res.push_back(path);
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举该位置可以放哪些数
        {
            if (!st[i]) 
            {
                path[u] = nums[i];
                st[i] = true;
                dfs(nums, u + 1);
                st[i] = false;
                while (i + 1 < nums.size() && nums[i + 1] == nums[i]) i ++; //跳过相同的数
            }
        }
    }
};