题目描述

给定一个包含 0 和 1 的二维网格地图，其中 1 表示陆地 0 表示水域。

网格中的格子水平和垂直方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

 

示例 :

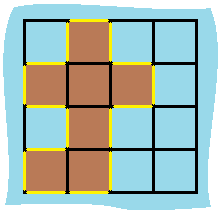
输入:
[[0,1,0,0],
 [1,1,1,0],
 [0,1,0,0],
 [1,1,0,0]]

输出: 16

解释: 它的周长是下面图片中的 16 个黄色的边：

算法1

刚开始想的是BFS遍历，遇到岛屿后查看四个方向是否有其他岛屿，否则该岛屿块的边就是岛屿周长之一。

C++ 代码

class Solution {
public:
    int addx[4] = { 0,0 ,1,-1 };
int addy[4] = { 1,-1,0,0 };

int vis[150][150] = { 0 };
queue<pair<int, int>> Q;
int bfs(vector<vector<int>>& grid) {
    int ans = 0;
    //bfs
    while (Q.size())
    {
        int x = Q.front().first;
        int y = Q.front().second;
        Q.pop();

        for (int i = 0; i < 4; i++) {
            int newx = x + addx[i];
            int newy = y + addy[i];

            if (newx >= 0 && newx < grid.size() && newy >= 0 && newy < grid[0].size() &&
                grid[newx][newy] == 1 && vis[newx][newy] == 0) {
                vis[newx][newy] = 1;
                Q.push({ newx,newy });
            }
            else if(newx >= 0 && newx < grid.size() && newy >= 0 && newy < grid[0].size() && 
                grid[newx][newy] == 1 && vis[newx][newy] == 1){
                //如果grid[x][y]周边的grid[newx][newy] 是岛屿 只不过是已经遍历过得 那么
                //grid[x][y]的边不作为岛屿周长
            }
            else {
                //如果grid[x][y]周边的 grid[newx][newy] 不是岛屿  或者是越界的面积 
                //grid[x][y]那么这个边就作为岛屿的周长
                ans++;
            }
        }
    }

    return ans;
}

int islandPerimeter(vector<vector<int>>& grid) {

    for (int i = 0; i < grid.size(); i++) {
        for (int j = 0; j < grid[0].size(); j++)
        {
            //找到第一个岛屿 作为bfs入口
            if (grid[i][j] == 1) {
                Q.push({ i,j });
                vis[i][j] = 1;
                return bfs(grid);
            }
        }
    }


    return 0;
}
};

算法2

后面发现 不BFS 直接暴力遍历整个矩阵 发现岛屿块 检测上下左右四个方向即可

C++ 代码

class Solution {
public:
    int dx[4] = {0, 1, 0, -1};
    int dy[4] = {1, 0, -1, 0};
    int islandPerimeter(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size(), ans = 0;

        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                if (grid[i][j] == 1) {
                    int tot = 4;
                    for (int d = 0; d < 4; d++) {
                        int tx = i + dx[d], ty = j + dy[d];
                        if (tx < 0 || tx >= n || ty < 0 || ty >= m)
                            continue;

                        if (grid[tx][ty] == 1)
                            tot--;
                    }
                    ans += tot;
                }
        return ans;
    }
};