算法

(并查集) $O(n^2)$

可以考虑染色法，最开始，每个人都有自己的颜色。

若知道了$A$和$B$是亲戚：

• 如果$A$与$B$同色，则不管；
• 否则将所有颜色为$B$的人染成$A$的颜色。

对于询问操作，只需要判断$A$和$B$是否为同一颜色。

改进：我们可以不去执行染色操作，而是给$B$设置一个标记指向$A$，说明它应该被染成$A$的颜色。

例如：

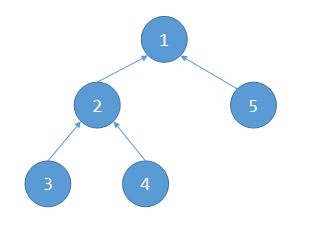
$Link\ 1\ 2$
$Link\ 2\ 3$
$Link\ 2\ 4$
$Link\ 1\ 5$

最后：$bin[1]=1,bin[2]=1,bin[3]=2,bin[4]=2$

这样，我们可以通过查询$bin$数组，来知道点x最后应该被染成什么颜色。
那么我们应对$Ask$询问就很简单了：去找$A,B$各自的颜色，然后判断这两个颜色是否相同。
如果相同，就有亲属关系；如果不同，就没有。

把本题抽象一下，将有亲属关系的人视为集合。
把一个集合的$bin$最终指向的那个元素，称为这个集合的代表。

可以发现，我们实现了这样一个功能：

• $Union$ 将两个（不相交的）集合合并
• $Find$ 查询一个元素所在集合的代表（进而可以实现$Ask$）

时间复杂度

单次询问的时间复杂度为$O(n)$,可以用路径压缩降为$O(\alpha(n))$，而$\alpha(n)\approx 4$，所以可认为是$O(1)$。
另外，本题的数据范围比较小，$O(n^2)$就能过。

C++ 代码

#include <iostream>

using namespace std;

struct unionFind {
    int bin[100010];

    unionFind() {
        for (int i = 1; i <= 100007; ++i) bin[i] = i;
    }

    int anc(int x) { // 查询x最终被染成什么颜色 
        if (bin[x] == x) return x;
        return anc(bin[x]); 
    }
    void uni(int x, int y) { // 把两群人染成同一种颜色 
        bin[anc(x)] = anc(y);
    }
    void ask(int x, int y) {
        cout << (anc(x) == anc(y) ? "Yes" : "No") << '\n';
    }
};

unionFind u;

int main() {
    int n, m, p;
    cin >> n >> m >> p;

    int x, y;
    while (m--) {
        cin >> x >> y;
        u.uni(x, y);
    }

    while (p--) {
        cin >> x >> y;
        u.ask(x, y);
    }
    return 0;
}