题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
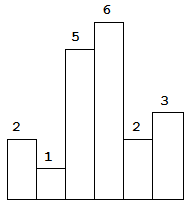
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
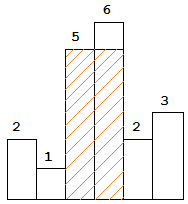
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例
输入: [2,1,5,6,2,3]
输出: 10
算法1
暴力枚举 $O(n^3)$
从最基本的暴力枚举开始,对于这道题,我们需要勾勒出最大矩形面积,我们可以进行两次遍历,找到任意两根柱子之间的的面积,并更新最大值。对于任意两根柱子,我们还需要再循环一遍两根柱子之间的所有元素,找到最矮的那根,作为矩形的高。该思路比较简单,但是需要三重循环,时间复杂度较高,具体代码就不实现了。
暴力优化 $O(n^2)$
让我们换一个思路,因为需要找到最大矩形区域,当我们勾勒出最大矩形时,该矩形的高一定是某一根柱子的高度。然后它的左右边界就是这根柱子能够延申到的最远距离。换句话说,对于每一根柱子,我们都能找到以它的高度为宽的最大矩形。同时它的左右边界,就是它两侧第一次出现的比该柱子更矮的柱子。所以当我们可以遍历每一根柱子,然后再向左遍历找到它的左边界,同时向右遍历找到它的右边界。最后就可以找到完全包含该柱子的最大矩形区域了。
对于这种优化之后的暴力,我们枚举的第一维是所有元素,第二维是以该元素为基准,分别向两侧延申,因此该暴力算法的时间复杂度是平方级别,较第一种有了很大的提升。实现代码如下:(很遗憾,该算法虽然很简单,但是还是超时了)
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int maxv = 0;
for (int i = 0; i < heights.size(); i ++)
{
int left = i, right = i;
while (left >= 0 && heights[left] >= heights[i]) left --;
while (right < heights.size() && heights[right] >= heights[i]) right ++;
maxv = max(maxv, heights[i] * (right - left - 1));
}
return maxv;
}
};
单调栈优化 $O(n)$
单调栈相关知识及基础题型建议阅读:
LeetCode 739. 每日温度
LeetCode 496. 下一个更大元素 I
LeetCode 503. 下一个更大元素 II
那么我们为什么会想到应用单调栈来解决这道问题呢?
因为在升级的暴力解法中,我们每次都需要重新确定一根柱子的左右边界。其实当我们从左往右遍历柱子时,我们每次遍历时我们已经获取了左侧和右侧所有柱子的高度信息。根据之前对单调栈的介绍,单调栈可以通过一次遍历,找出每个元素的上一个更小或下一个更大元素。因此我们想到利用单调栈先对元素进行预处理,先求出每根柱子左边第一个更矮以及右边第一个更矮的柱子,然后再进行一次循环遍历所有元素,即可得到面积最大值。具体步骤如下:
- 我们栈中元素存储的是下标,而对于两端的柱子,它们两侧的边界分别为
-1和n,因此在循环处理之前我们需要在单调栈里先放入边界元素。 - 先从左往右循环,找到每个元素左边第一个比它矮的元素,并放入
left数组。再从右往左循环,找到右边第一个比它矮的元素,并放入right数组。 - 最后循环所有元素,更新最大面积。
利用单调栈,我们实际上只需要对数组进行三次遍历,因此时间复杂度优化到了$O(n)$
C ++代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> stk_l, stk_r;
int n = heights.size();
vector<int> left(n), right(n);
stk_l.push(-1);
for(int i = 0; i < n; i++)
{
while(stk_l.top() != -1 && heights[i] <= heights[stk_l.top()]) stk_l.pop();
left[i] = stk_l.top();
stk_l.push(i);
}
stk_r.push(n);
for(int i = n - 1; i >= 0; i--)
{
while(stk_r.top() != n && heights[i] <= heights[stk_r.top()]) stk_r.pop();
right[i] = stk_r.top();
stk_r.push(i);
}
int res = 0;
for(int i = 0; i < heights.size(); i++) res = max(res, heights[i] * (right[i] - left[i] - 1));
return res;
}
};
单调栈再优化
在上述利用单调栈的过程我们可以发现,我们对原数组进行了三次遍历,其中两次是从左往右的遍历,还有一次从右往左的遍历,那么我们的遍历的次数还能够再进行优化吗?答案是肯定的。
回顾一下上面计算某元素左边第一个更小元素的过程,我们从左往右遍历数组中的每个元素,当栈顶元素大于等于该元素时,就不断弹出,直到小于该元素时,此时的栈顶元素就是左边第一个更小的元素,然后我们将栈顶元素记录在数组中,再放入该元素。
所以当我们从左往右更新单调栈时,栈中存储的每个元素的上一个元素就是它左边第一个更小元素。因此当我们每次弹出一个元素时,如果我们同时又可以知道它右边第一个更小的元素,我们就可以直接更新最大面积了。
那么它右边第一个更小元素是谁呢? 其实就是我们遍历到的该元素。因为我们是按照从左往右的顺序依次遍历每个元素,所以遍历到的比栈顶元素更小的元素必然是右边第一个更小元素。
最后,我们的单调栈可能还未空,是因为数组中没有比栈中元素更小的数了,此时它们的右边界就是n,此时我们仍需将它们弹出并更新面积最大值。
通过上面的分析,我们就可以只通过一次循环遍历,求出最大面积了。
C ++代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> stk;
int n = heights.size();
int res = 0;
stk.push(-1); //放入边界
for(int i = 0; i < n; i++)
{
while(stk.top() != -1 && heights[i] <= heights[stk.top()])
{
int j = stk.top(); //弹出栈顶元素, 左边界为此时栈顶,右边界为该遍历元素
stk.pop();
res = max(res, heights[j] * (i - stk.top() - 1));
}
stk.push(i);
}
while (stk.top() != -1)
{
int j = stk.top();
stk.pop();
res = max(res, heights[j] * (n - stk.top() - 1)); //右边界为`n`
}
return res;
}
};
分治法
该方法就没有前面的方法那么直观了,在 排序算法总结 中介绍了快速排序的分治思想。对于这道题,我们也可以利用类似的分治思想,每次找到数组中高度最矮的那根柱子,然后接下来最大矩形区域就是下面的几种情况了:
- 最大矩形区域在不包含选定柱子的左半区域当中。
- 最大矩形区域在不包含选定柱子的右半区域当中。
- 最大矩形区域包含选定柱子的区域。
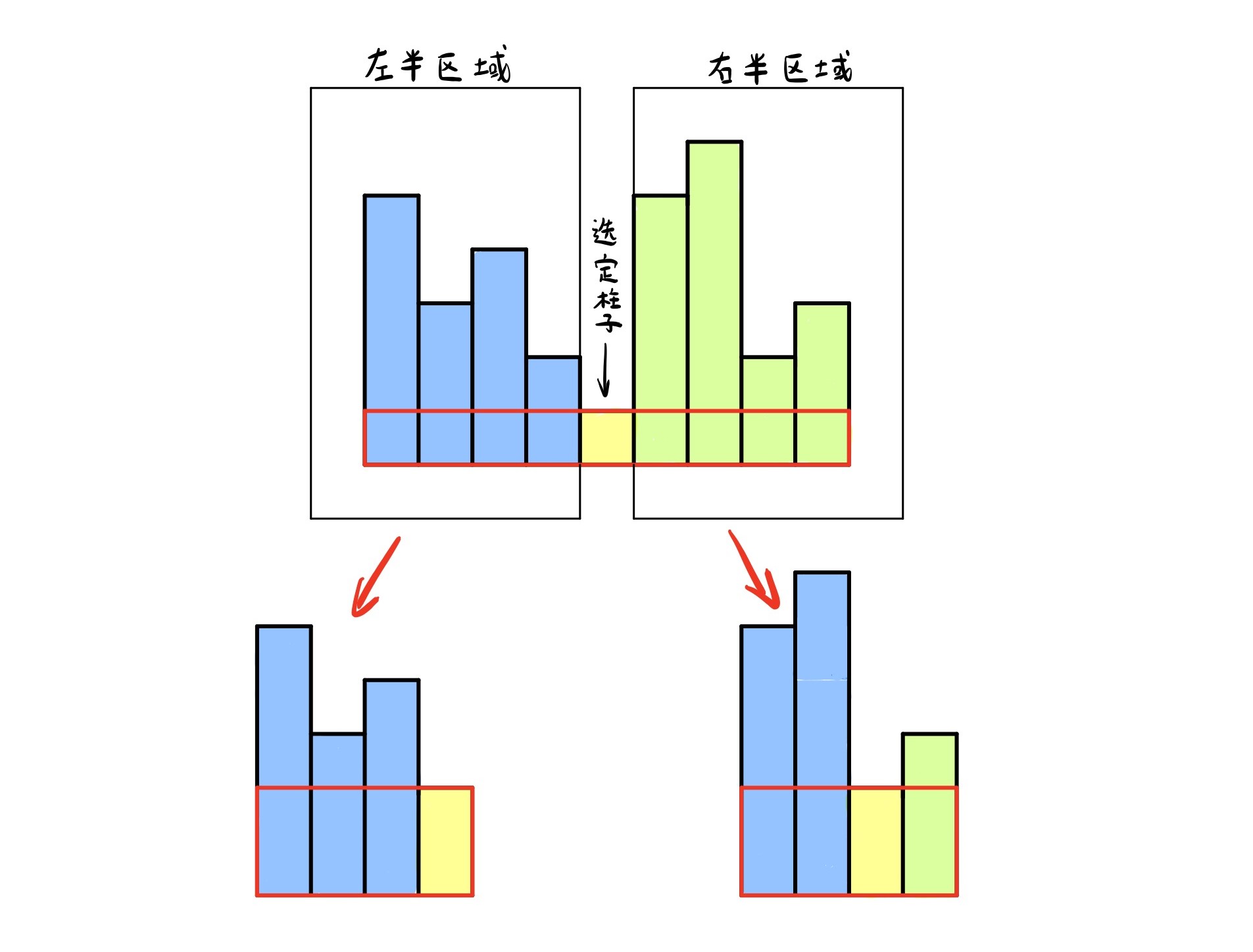
所以用分治法求解的思路就是首先找到所有柱子中最矮的那根,此时包含它的最大矩形区域的宽度为整个数组宽度。然后利用下标,求出包含该柱子的最大矩形区域。之后我们分别再对其左右两边区域调用函数求解,返回左右两侧区域的最大矩形面积,最后将三种面积进行比较,得到最大面积。
由于每次需要查询一个区间的最小值,最简单的办法是循环,时间复杂度较高,要么可以使用RMQ算法,过程又比较繁琐了,在这里就不把代码贴出来了,具体感兴趣的同学可以自己尝试写一下代码。关于RMQ算法的题目 1273. 天才的记忆


对于每一根柱子,我们都能找到以它的高度为宽的最大矩形,爱了
力扣上还有个最大矩形也是单调栈的变种