题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接6个单位的雨水（蓝色部分表示雨水）。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

暴力枚举

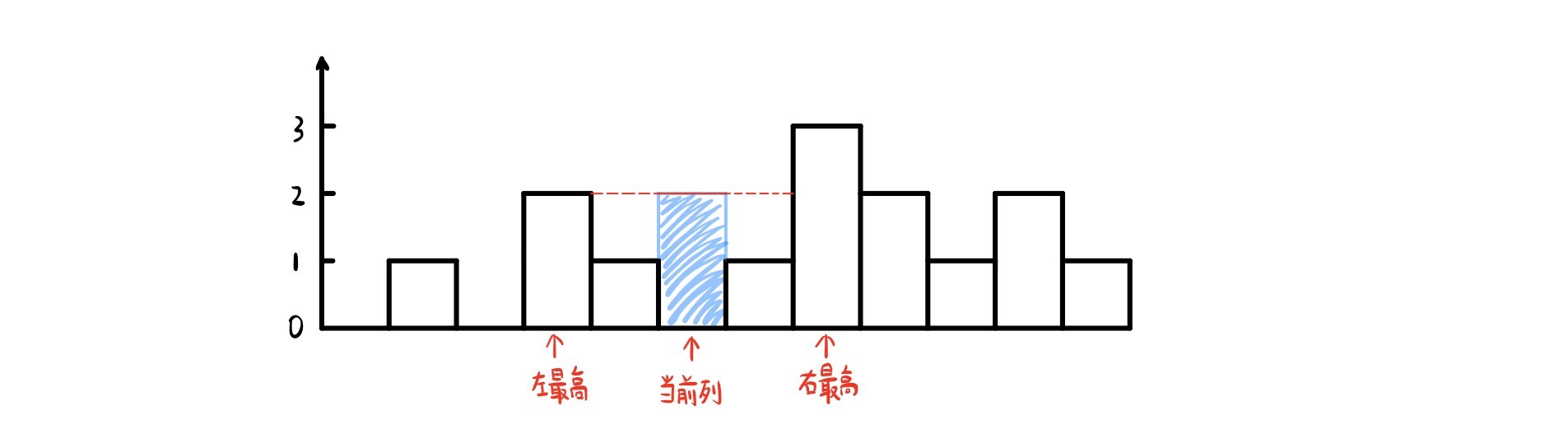
从图中可以看到，蓝色部分就是能够接到的雨水。对于任何一列，能够接到雨水的条件就是在它的左右侧存在比当前列高度更高的柱子。同时，根据木桶效应，能够装水的高度取决于左右两侧最高的柱子中较矮的那一根。

所以我们最基本的暴力思路就有了，从左往右遍历每一列。同时对每一列再分别向左和向右进行第二层遍历，找到它左右高度最高的柱子。其实，由于第一列和最后一列的两边都没有柱子，所以我们遍历时只需要从下标1到height.size() - 2就可以了。该枚举思路类似于 LeetCode 84. 柱状图中最大的矩形中暴力枚举的思路，大家可以参考一下。

对于每一列，我们有以下几种情况：

1. 两侧都能够找到比当前列高的柱子
2. 两侧都不存在比当前列更高的柱子
3. 只有一侧存在比当前列更高的柱子

对于情况一，当然是我们最希望看到的。在情况二和三下，均不能满足接水条件。但其实我们在写代码时，可以将三种情况考虑在一起。我们先假设left_max和right_max均为当前柱子的高度。当我们没有找到两侧更高的柱子时，此时两侧柱子中的较矮值减去当前柱子的高度即为0，意味着情况二和情况三都不能够满足装水条件，此时并不会更新我们的答案。

$O(n^2)$的时间复杂度，大概率是个超时算法，接下来还是想想怎么优化吧。

暴力优化

我们注意到，其实在上面的暴力枚举中，我们每遍历一个列时，我们都需要向它的两侧进行遍历来找到左右最高的柱子。但其实在这过程中我们对一些相同数据进行了多次重复遍历，消耗了多余的时间，

我们可以运用两个数组来分别存储每一列左侧和右侧的最高柱子。但是注意 这里的最高柱子并没有与当前列进行比较。所以在找到两侧最高柱子中较矮的柱子时，还需要判断其是否与当前列的高度高，如果高，才能满足接水的条件。

C ++代码

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) return 0;
        int n = height.size();
        vector<int> left(n);
        vector<int> right(n);

        left[0] = height[0];
        for (int i = 1; i < height.size(); i ++)
            left[i] = max(left[i - 1], height[i]);

        right[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i --)
            right[i] = max(right[i + 1], height[i]);

        int res = 0;
        for (int i = 1; i < n - 1; i ++)
        {
            int h = min(left[i], right[i]);
            if (h > height[i]) res += h - height[i]; 
        }

        return res;
    }
};

暴力再优化

其实在上面的暴力优化中，当我们从左往右遍历每一根柱子时，我们就可以不断更新其左侧柱子的最大值，进而直接使用。于是我们就想直接用一个变量将左侧最高柱子存储起来，不断更新，而不需要新分配一个数组。但是由于对右侧柱子高度的未知，我们还是需要用一个数组记录每根柱子右侧最高柱子的信息。

该办法与上一个时间复杂度一样，但是空间复杂度得到了一定的优化。

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) return 0;
        int n = height.size();
        vector<int> right(n);

        right[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i --)
            right[i] = max(right[i + 1], height[i]);

        int res = 0;
        int maxv = height[0];
        for (int i = 1; i < n - 1; i ++)
        {
            int h = min(maxv, right[i]);
            if (h > height[i]) res += h - height[i]; 
            maxv = max(maxv, height[i]);
        }

        return res;
    }
};

双指针算法

在LeetCode 11. 盛最多水的容器 介绍了利用双指针来求解盛水问题，同样是接水问题，那么这道题可不可以用双指针来解决呢？答案是肯定的。

两根柱子之间能够接到的水，依据木桶效应，不论它们之间距离多远，之间能够接到水的多少肯定取决于较矮的那根。所以我们比较两根指针指向的高度，每次把较矮的指针向中间移动。同时在移动指针时还需要考虑该指针是否有下沉，因为如果高度有下降则表示能够接到水，此时我们就更新我们的雨水值。

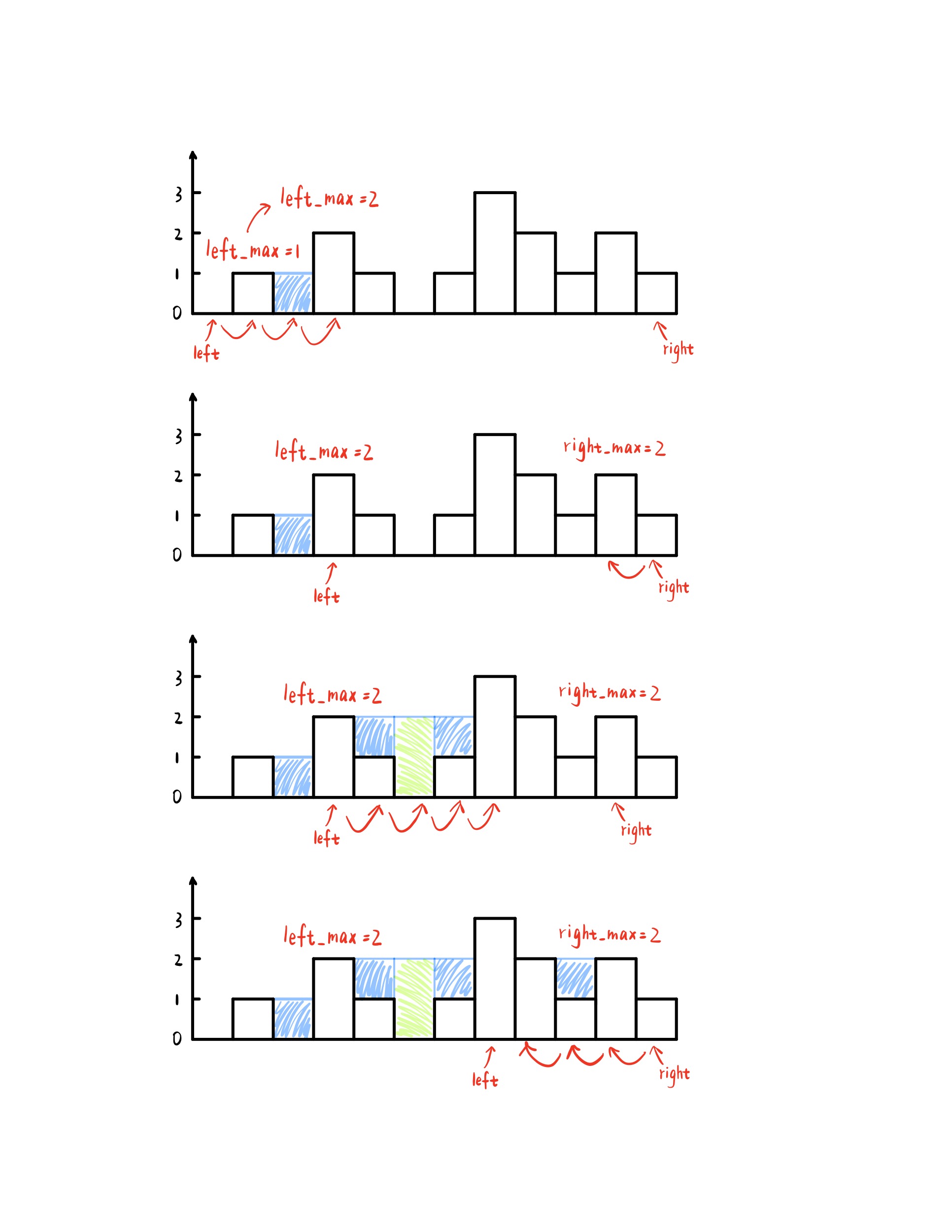
class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) return 0;
        int n = height.size();
        int left_max = 0, right_max = 0;
        int l = 0, r = n - 1, res = 0;
        while (l < r)
        {
            if (height[l] <= height[r])
            {
                if (height[l] >= left_max) left_max = height[l];
                else res += left_max - height[l];
                l ++;
            }
            else{
                if (height[r] >= right_max) right_max = height[r];
                else res += right_max - height[r];
                r --;
            }
        }

        return res;
    }
};

单调栈

关于单调栈的具体实现与题目：
LeetCode 739. 每日温度
LeetCode 496. 下一个更大元素 I
LeetCode 503. 下一个更大元素 II
LeetCode 84. 柱状图中最大的矩形

其实这道题思路与84题比较类似，84题中为了求以某一根柱子高度为矩形宽度的矩形最大值，我们需要找到柱子两侧的第一个更小元素。对应于这道题，对于某一列，能够接水的的条件是两侧存在比当前列高的柱子，因此我们这道题也可以用单调栈求解了。

我们从左往右遍历数组，并用一个单调栈来记录每根柱子的下标。当被遍历到的柱子比栈顶元素矮，即说明该柱子可能满足接水条件（右侧是否有比当前更高的柱子未知），于是我们可以将它入栈。但是当栈顶元素遇到比它更高的柱子时，表明该栈顶元素的两侧边界已经找到。所以此时需要将其从栈中pop出，计算接水量。

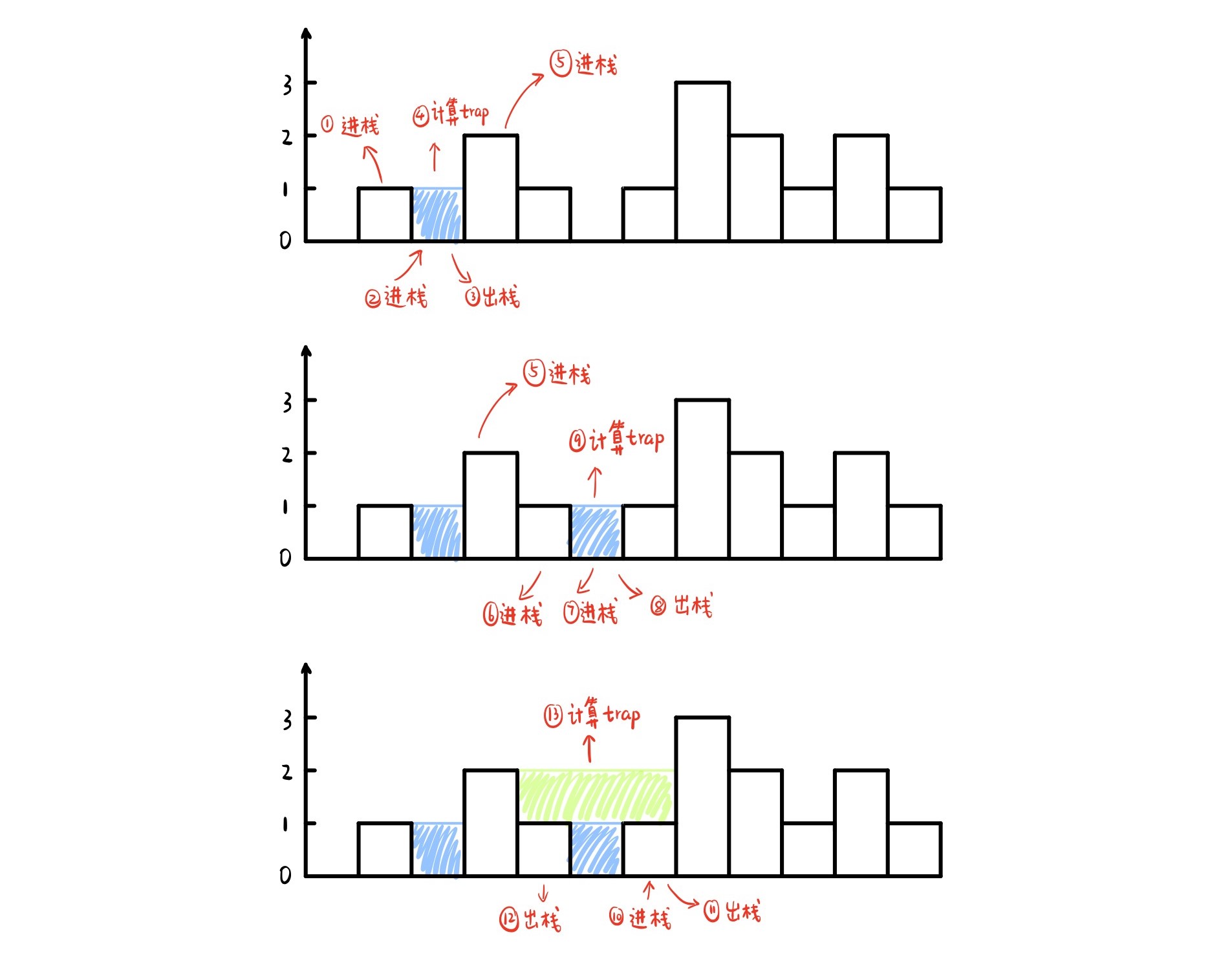
注意:

单调栈代码中答案res更新的计算公式为
res += (i - index.top() - 1) * (h - height[j])
该计算公式是按行计算的，而双指针法中trap的计算是基于列运算的。虽然计算结果肯定都一样，但是它们的计算原理有所不同。

C++代码

class Solution {
public:
    int trap(vector<int>& height) {
    int res = 0;
    stack<int> stk;
    stk.push(0);
    for (int i = 1; i < height.size(); i++) {
        while (!stk.empty() && height[i] > height[stk.top()]) {
            int j = stk.top(); 
            stk.pop();
            if (!stk.empty()) {
                int h = min(height[i], height[stk.top()]);
                res += (i - stk.top() - 1) * (h - height[j]);
            }
        }
        stk.push(i);
    }
    return res;
    }
};