KMP的个人理解和解析
题外话:刚刚学习KMP算法,一脸懵逼,不过经过一天的思考、查找资料、手动画图模拟啥的终于算是搞清楚了(可能吧,其实我心里也没底),在此写一篇解析整理一下思路。
一、什么是KMP算法及一些基本概念
首先,什么是KMP算法。这是一个字符串匹配算法,对暴力的那种一一比对的方法进行了优化,使时间复杂度大大降低(我不会算时间复杂度。。。,目前也只能这么理解,还有KMP是取的三个发明人的名字首字母组成的名字)。
然后是一些基本概念:
1、s[ ]是模式串,即比较长的字符串。
2、p[ ]是模板串,即比较短的字符串。(这样可能不严谨。。。)
3、“非平凡前缀”:指除了最后一个字符以外,一个字符串的全部头部组合。
4、“非平凡后缀”:指除了第一个字符以外,一个字符串的全部尾部组合。(后面会有例子,均简称为前/后缀)
5、“部分匹配值”:前缀和后缀的最长共有元素的长度。
6、next[ ]是“部分匹配值表”,即next数组,它存储的是每一个下标对应的“部分匹配值”,是KMP算法的核心。(后面作详细讲解)。
核心思想:在每次失配时,不是把p串往后移一位,而是把p串往后移动至下一次可以和前面部分匹配的位置,这样就可以跳过大多数的失配步骤。而每次p串移动的步数就是通过查找next[ ]数组确定的。
二、next数组的含义及手动模拟(具体求法和代码在后面)
然后来说明一下next数组的含义:对next[ j ] ,是p[ 1, j ]串中前缀和后缀相同的最大长度(部分匹配值),即 p[ 1, next[ j ] ] = p[ j - next[ j ] + 1, j ]。
如: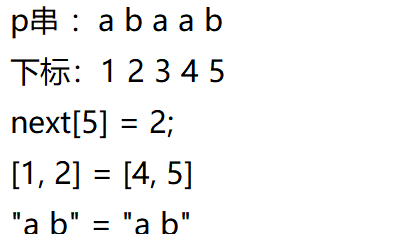
手动模拟求next数组:
对 p = “abcab”
| p | a | b | c | a | b |
|---|---|---|---|---|---|
| 下标 | 1 | 2 | 3 | 4 | 5 |
| next[ ] | 0 | 0 | 0 | 1 | 2 |
对next[ 1 ] :前缀 = 空集—————后缀 = 空集—————next[ 1 ] = 0;
对next[ 2 ] :前缀 = { a }—————后缀 = { b }—————next[ 2 ] = 0;
对next[ 3 ] :前缀 = { a , ab }—————后缀 = { c , bc}—————next[ 3 ] = 0;
对next[ 4 ] :前缀 = { a , ab , abc }—————后缀 = { a . ca , bca }—————next[ 4 ] = 1;
对next[ 5 ] :前缀 = { a , ab , abc , abca }————后缀 = { b , ab , cab , bcab}————next[ 5 ] = 2;
三、匹配思路和实现代码
KMP主要分两步:求next数组、匹配字符串。个人觉得匹配操作容易懂一些,疑惑我一整天的是求next数组的思想。所以先把匹配字符串讲一下。
s串 和 p串都是从1开始的。i 从1开始,j 从0开始,每次s[ i ] 和p[ j + 1 ]比较
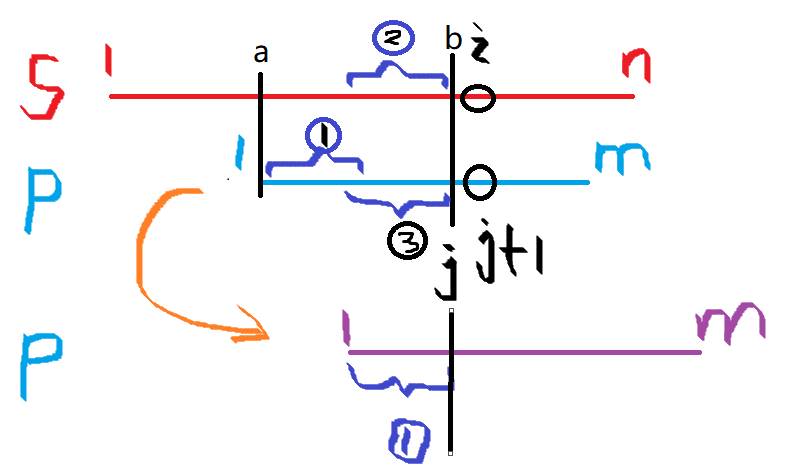
当匹配过程到上图所示时,
s[ a , b ] = p[ 1, j ] && s[ i ] != p[ j + 1 ] 此时要移动p串(不是移动1格,而是直接移动到下次能匹配的位置)
其中1串为[ 1, next[ j ] ],3串为[ j - next[ j ] + 1 , j ]。由匹配可知 1串等于3串,3串等于2串。所以直接移动p串使1到3的位置即可。这个操作可由j = next[ j ]直接完成。 如此往复下去,当 j == m时匹配成功。
代码如下
for(int i = 1, j = 0; i <= n; i++)
{
while(j && s[i] != p[j+1]) j = ne[j];
//如果j有对应p串的元素, 且s[i] != p[j+1], 则失配, 移动p串
//用while是由于移动后可能仍然失配,所以要继续移动直到匹配或整个p串移到后面(j = 0)
if(s[i] == p[j+1]) j++;
//当前元素匹配,j移向p串下一位
if(j == m)
{
//匹配成功,进行相关操作
j = next[j]; //继续匹配下一个子串
}
}
注:采用上述的匹配方法( i 与 j+1 比较)我不清楚(其实是想不清楚)为什么要这样。。。脑子有点不好使。而不推荐下标从0开始的原因我认为是:若下标从0开始的话,next[ ]数组的值都会相应-1,这就会导致它的实际含义与其定义的意思不符(部分匹配值和next数组值相差1),思维上有点违和,容易出错。
(看了习题课,在实际操作上下标从0开始代码会多很多东西,比从1开始复杂一些,嗯。。。确实
四、求next数组的思路和实现代码
next数组的求法是通过模板串自己与自己进行匹配操作得出来的(代码和匹配操作几乎一样)。
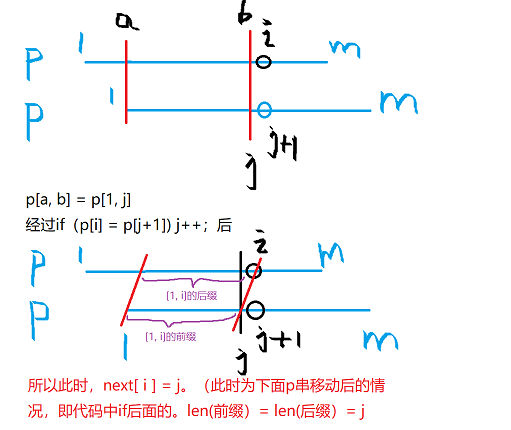
代码如下
for(int i = 2, j = 0; i <= m; i++)
{
while(j && p[i] != p[j+1]) j = next[j];
if(p[i] == p[j+1]) j++;
next[i] = j;
}
代码和匹配操作的代码几乎一样,关键在于每次移动 i 前,将 i 前面已经匹配的长度记录到next数组中。
五、完整代码
// 注:这不是题目的AC代码,是一个最基本的模板代码
#include <iostream>
using namespace std;
const int N = 100010, M = 10010; //N为模式串长度,M匹配串长度
int n, m;
int ne[M]; //next[]数组,避免和头文件next冲突
char s[N], p[M]; //s为模式串, p为匹配串
int main()
{
cin >> n >> s+1 >> m >> p+1; //下标从1开始
//求next[]数组
for(int i = 2, j = 0; i <= m; i++)
{
while(j && p[i] != p[j+1]) j = ne[j];
if(p[i] == p[j+1]) j++;
ne[i] = j;
}
//匹配操作
for(int i = 1, j = 0; i <= n; i++)
{
while(j && s[i] != p[j+1]) j = ne[j];
if(s[i] == p[j+1]) j++;
if(j == m) //满足匹配条件,打印开头下标, 从0开始
{
//匹配完成后的具体操作
//如:输出以0开始的匹配子串的首字母下标
//printf("%d ", i - m); (若从1开始,加1)
j = ne[j]; //再次继续匹配
}
}
return 0;
}
六、小结
这是我开始学算法以来(虽然也没几天。。。)遇见的第一个非常头疼的算法,纠结了一天,强行一步一步手动模拟画图慢慢想通(果然脑袋转的太慢了),非常爽,哈哈~~
(虽然说还是有很多小细节没想清楚,脑袋一想这东西就宕机了。。。
希望能够从此开始,在编程的路上越走越远 ^_^
七、参考
1、 AcWing算法基础课。
2、字符串匹配的KMP算法——前缀和后缀的详解, 作者:阮一峰


这玩意像老鼠屎一样,万年难得一用,不用细节就忘,忘了又回来看,过半年又忘
太真实了
太真实了 过了几个月我又用到了 又忘了
兄弟,你这么形容,我很难不赞同。
深有同感🥺
# 来来复复看了好几次了都
真实!!
太对了哥们 😭
好喻,同感!
我一年半前写的了,现在又不会了hhh
关于为什么求next数组和匹配的操作类似(理解仅供参考
因为本质是一样的:对于S串每一个特定的下标i,在满足s[i-j+1,i]=p[0,j]的前提下,我们需要找出j的最大值
唯一不同的在于,求next数组时,我们关心对于每个不同的下标i,j能走多远;匹配时,我们只关心j是否走到末尾
非常有意思的说法是,
求next数组时:对于每个i:“j走到哪了呀?我用数组记录一下你的位置”
匹配时:对于每个i:“到终点和我说声,匹配完我输出一下,没事别叫我。”
说得好!
6 说的好
666
大佬讲得蛮好的,我这里对 next 数组还有一些补充,有疑惑的同学可以看下~
https://www.acwing.com/file_system/file/content/whole/index/content/6255932/
j = ne[j]; //再次继续匹配
能具体解释一下吗大佬?
只有j走到末尾的时候,才会执行
j=ne[j];,也就是说此时已经找到了p在s中出现的下标,但后面还可能出现,因此要继续匹配继续往后匹配的话,s串的下标
i要后移,刚好结束循环时会++,那不用管;除此之外p串的下标j也要倒回去匹配,所以要将其手动倒回到上一个可能匹配的地方(ne[j]就是上一个可能匹配的地方)补充一下八个月前的评论:求next数组时,上述的s和p串都是模式串p自己;匹配时的p和s和题目描述一样;当时我的视角应该是把使用
i下标的串叫做s,使用j下标的串叫做pvocalvocal好妙的想法
这个解释无敌了
模式串和模板串好像说反了
好像确实反了(?
我看半天人都傻了,后面才反应过来
叫主串和模式串就不会有歧义了
KMP算法的核心是双指针、数组和递推,用双指针可以提取重复的长度,用数组可以保存重复的长度,用递推可以指导怎样去缩小重复的长度。
KMP算法的思路主要是用空间换时间,传统方式进行搜索,一旦匹配失败,模式串就需要重新开始匹配,KMP算法就是从怎样减少回退进行考虑的。
在KMP算法的双指针中,指针i用于扫描主串,指针j既用于扫描模式串。
当在第j个位置匹配失败的时候,需要回退到以j-1为最后一个元素的序列中以前后缀长度为下标的后一个元素,
因为是从0开始的,那么只需要用next保存以当前元素为最后一个元素的序列的相同前后缀的长度即可。
对于模板串$abcab$,
按照非平凡前后缀相等的关系:$\begin{array}{c|c|c|c|c|c}串&a&b&c&a&b\\\ \\hline 数组下标&1&2&3&4&5 \\\ \\hline next[] &0&0&0&1&2 \end{array}$,即$y$总所讲。
按照王道的解法,$next[1]\\equiv 0,next[2]\\equiv 1$,那么:$\begin{array}{c|c|c|c|c|c}串&a&b&c&a&b\\\ \\hline 数组下标&1&2&3&4&5 \\\ \\hline next[] &0&1&1&1&2 \end{array}$
当数组下标要从$1$开始时,把王道的讲法中$next[]$数组集体减$1$即可。
结果不同的原因是$next[]$数组在这里的含义是匹配失败后,下一次$j$指针要指向哪里开始匹配。
这里解释下$c$,同理$2$号位的$b$,$4$号位的$a$也是同理。$?$是匹配失败的位置,$\ast$是已匹配过的位置。
$\begin{array}{ccccccc|ccc}指针&&&&&&&i&& \\\ \\hline原串&\ast &\ast &\ast &\ast &a& b&? & &\\\ \\hline 模板串&&&&&a&b&c&a&b \\\ \\hline 指针 &&&&&&&j&&\end{array}$,这个位置匹配失败时,把模板串依次向右移动,
$\begin{array}{ccccccc|ccc}指针&&&&&&&i&& \\\ \\hline原串&\ast &\ast &\ast &\ast &a& b&? & &\\\ \\hline 模板串&&&&&&a&b&c&a \\\ \\hline 指针 &&&&&&&j&&\end{array}$,然而已知的竖线前面$b$与$a$不匹配,继续右移
$\begin{array}{ccccccc|ccc}指针&&&&&&&i&& \\\ \\hline原串&\ast &\ast &\ast &\ast &a& b&? & &\\\ \\hline 模板串&&&&&&&a&b&c \\\ \\hline 指针 &&&&&&&j&&\end{array}$,此时已经到头,$j$指针指向的是下标为$1$的$a$,所以$next[3]=1$。
对于最后一个$b$:如下表,移动的最终位置,指针$j$指向第二个$b$,所以$next[5]=2$
$\begin{array}{ccccccccc|c}指针&&&&&&&&&i \\\ \\hline原串&\ast &\ast &\ast &\ast &a& b&c &a &?\\\ \\hline 模板串&&&&&a&b&c&a&b \\\ \\hline 指针 &&&&&&&&&j\end{array} \\Rightarrow \begin{array}{ccccccccc|cccc}指针&&&&&&&&&i&&& \\\ \\hline原串&\ast &\ast &\ast &\ast &a& b&c &a &?&&&\\\ \\hline 模板串&&&&&&&&a&b&c&a&b \\\ \\hline 指针 &&&&&&&&&j\end{array}$
然而实际在$408$考研真题中从未出现过需要完整写出$next$数组。
ps:不知道为什么\和\hline的斜杠需要写成双斜线才可以显示出来,可能类似于需要转义吧233333
至于上面的$next[1]\\equiv 0,next[2]\\equiv 1$是根据其代码实现规定的。
但对于非平凡前后缀相等长度中,仅有$next[1]\\equiv 0$恒等于0,这是因为非平凡字串所限制的。
比如wd课程中给出的字符串$google$的next数组是:$\begin{array}{c|c|c|c|c|c|c}串&g&o&o&g&l&e\\\ \\hline 数组下标&1&2&3&4&5&6 \\\ \\hline next[] &0&1&1&1&2&1 \end{array}$
而按照前后缀长度相等得出的next数组是:$\begin{array}{c|c|c|c|c|c|c}串&g&o&o&g&l&e\\\ \\hline 数组下标&1&2&3&4&5&6 \\\ \\hline next[] &0&0&0&1&0&0 \end{array}$
以上讨论都是在next数组下标从1开始,仅仅是两种解法对于next数组的定义有所不同,所以相应的数组值以及代码的实现都有所不同。
更正:第$4$行:”当数组下标要从$1$开始时”,改为”当数组下标要从$0$开始时”
非常感谢,我还在奇怪为什么和书上的next数组不一样呢
但是为啥王道的解法和楼主的前缀后缀解法算出来不一样呢?视频里ababaa,ne[6]=4,用楼主这样算不对啊
用部分匹配值来算ne[6],前缀[a,ab,aba,abab,ababa],后缀[a,aa,baa,abaa,babaa],共有长度为为1,ne[6]=1啊,为啥和王道算出来的ne[6]=4不一样啊!
兄弟为啥啊,我也疑惑
王道的ne[j]实际上等于y总的ne[j - 1] + 1
王道408的书里y总的next[]数组实际上是书中写道的PM表,王道书中说使用PM表(也就是y总的next[]数组),每次匹配失败就要寻找前一个的部分匹配值,不方便,所以将PM表整体右移一位,next[0]=-1,在整体加1,就是书中的next[]数组。
具体的可以看下这篇博客,https://blog.csdn.net/coding_with_smile/article/details/125521122
按照上面那篇博客所写,大概率就是next,nextval,knext数组这个关系
CSDN的文章看不到图,这个可以
http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
可以
可以
next[i] = j;难懂
i为什么要从2开始
只有字符串长度大于1的时候,才会存在非平凡前后缀。next[1]的值固定是0
那就算是0假设next[2]也是0不就放进去一块算也行把
没懂您的意思。
从1开始,一定会把next数组变成1、2、3、。。。。
next[1]虽然是多余的但是也有结果是0啊
next[1]没有前缀
初始全局变量的int数组的时候,自动赋值值是0 的
https://www.seayj.cn/articles/99ba/
如果这个版本很难懂,可以把大脑放空,然后看我的文章和对应的 B 站视频。我一开始听得一脸懵,看自己以前的文章才看懂😅
next数组就是p串自身的性质,比如说
p串是abaabababa
s串是abaabbabababb
next[5]=2,意思是第一个字符到第五个字符之间,前缀与后缀相同的最大长度,前边有个ab后边有个ab嘛,并且也是能找到最长的,这玩意怎么用呢?假如p串前5个字符匹配成功,第六个失败了,是不是可以令j(5)=next[j](2),再将此时的i(6)与j+1匹配,这个过程相当于p串通过这个性质变成了
abaabababa
abaabbabababb
再就可以将p串第三个a(对应j+1)与刚刚的i(6)也就是b进行对比。
补:这个过程p串往后挪其实在代码上为i与j的映射关系
(这是我的理解😘)
所以每次比对失败了就挖掘一下已经成功匹配的p串的那部分的这个性质给匹配过程提提速
当某个字符匹配失败,i不再回退,只有j往后回退到next[j],这样在某些情况下会不会错过正确答案?
例如,上面第6个字符匹配失败,继续从p串第3个和s串第6个开始匹配,
会不会在s串2–5个之间也有能跟p串前面相匹配的?
我意思是,KMP这种做法固然免去了暴力算法的每一步比较,但会不会跳过太多导致错过?
这一点我没想明白…
在其他地方看到相关解释,差不多明白了。举个例子:
对s串A B C D A B C A B C D
对p串A B C D A B D
二者前6个字符匹配,第7个不匹配,需要回退,那么p串应该往右移动几步继续和s串匹配呢?
next数组告诉我们next[6] = 2 (即p串前缀AB == 后缀AB),故p串往右移动4步继续匹配:
之前我的疑问是,p串往右移动1步,2步行不行?比如移动1步
答案是不行。用反证法,假如s串后缀B C D A B和p串前缀A B C D A匹配,由next数组的定义,
此时next[6]应该是5而不是2,矛盾。移动2步,3步同理。因此,p串按next数组回退不会出现漏的情况。
感谢,总算看懂了
好形象,赞👍
好棒啊,我也是初学者,我昨天搞了半天基本原理和模拟都没问题,也看了一些博客之类的,还是你写的更简单易懂(可能同样是初学者吧)
将 i 前面已经匹配的长度记录到next数组中。这句话启发到我了
这篇题解特别好,像我一样的菜鸡也能懂。
大佬好厉害,咕噜灵波~
求next有点像动态规划呗,用前一步结果推后一步结果
求next有点像动态规划呗,用前一步结果推后一步结果
写一下自己对暴力算法的s[i + j - 1] != q[ j ]理解:
个人理解:s[i + j - 1] != q[ j ] 这个代码是判断字符串是否匹配,为什么是i + j -1? 是因为这里是两层循环如果是i的话 无法完成字符匹配(模拟一下就可以),i + j -1是为了在第二层循环中实现数组s和q都同时向前走,从而实现字符串匹配,直到没有匹配的字符之后会跳出进行下一层循环。
问下 怎么理解cin>>s+1 >>p+1 是表示循环从i=1 到n 依次输入字符串吗
数组的数组名是数组的首地址,也就是下标为0的位置,+1就从下标为1的位置开始
就不能写全?bug改好几年全靠你了
qaq