题目描述

实现int sqrt(int x)函数。

计算并返回x的平方根，其中x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,由于返回类型是整数，小数部分将被舍去。

算法思路

模板一

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

模板二

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

二分模板的使用方法和理解可点击二分套路总结

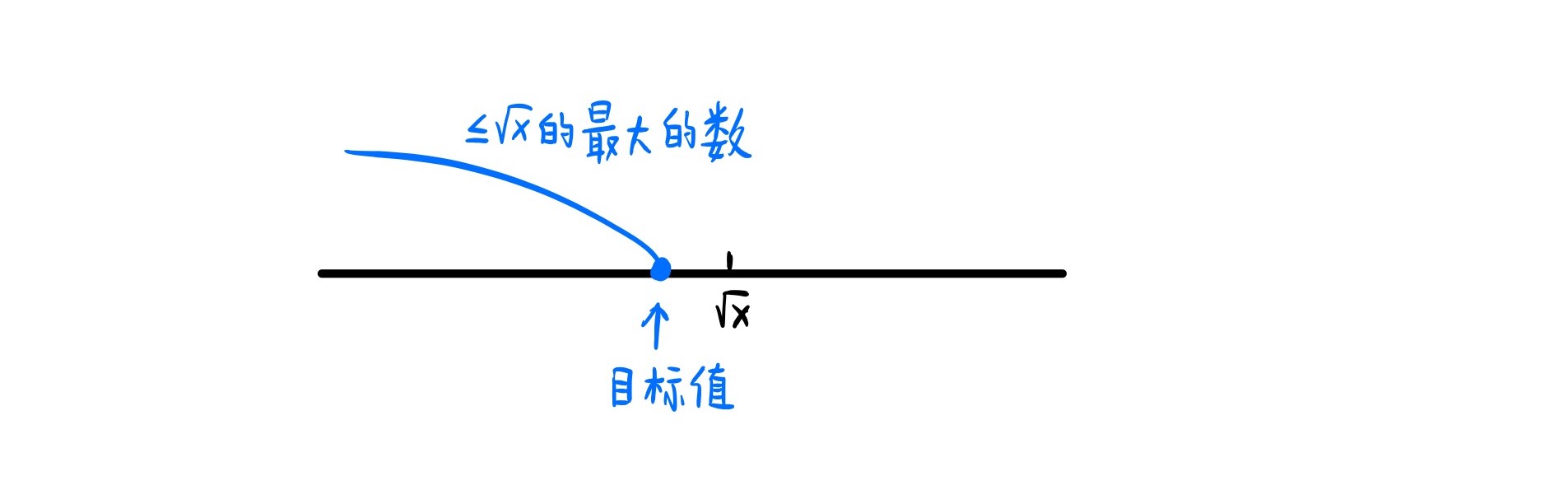
该题需要返回一个数x平方根的整数部分，如果一个数的平方根刚好是整数，那么我们的答案就是根号x,但是如果根号x是一个小数的话，我们需要返回的就是小于根号x的最大的整数，因此将上述两种情况合并起来，就可以得到和上面一样的二分求解区间，继续套用我们的模板二，即可求解。

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x;

        while(l < r)
        {
            int mid = l + (long long)r  + 1 >> 1;
            if(mid <= x / mid) l = mid;
            else r = mid -1;
        }
        return r;
    }
};