题目描述
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是O(logn) 级别。
示例 1:
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1
算法思路
二分套路 + 模板 (可参考 二分套路总结 )
在 LeetCode 153. 寻找旋转排序数组中的最小值 中我们已经发现,对于一个没有重复元素的旋转数组,会由于断层的出现,整个区间被一分为二。
该题要求我们在旋转数组中找到目标值,如果是对一个排序数组来说,这就是一个最简单的二分问题,对于旋转数组来说,整个区间由两个递增区间拼接而成,因此我们想到在两个区间里分别去找是否存在我们的目标值。
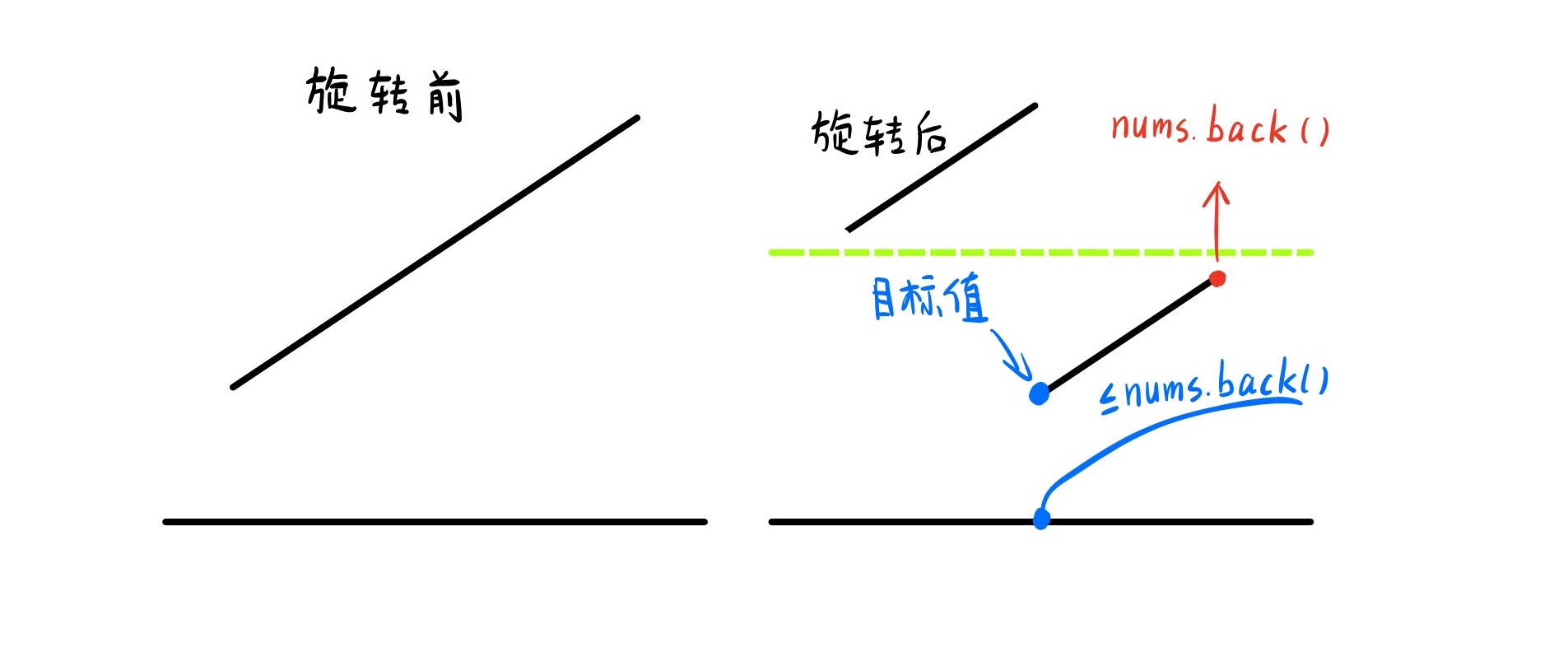
那么为了找到两个区间,我们就需要找到它们的分界点。根据下图我们知道分界点其实就是最小值。所以我们就根据LeetCode 153. 寻找旋转排序数组中的最小值的思路先求出最小值。然后判断我们目标值应该去哪个区间里找。
判断我们目标值与最后一个元素的大小关系,如果目标值比最后一个元素大,说明只可能出现在前半部分,反之,如果比最后一个元素小,则只可能出现在后半段。缩小区间后,在区间再做一次二分查找即可。
C++ 代码
class Solution {
public:
int search(vector<int>& nums, int target) {
if (nums.empty()) return -1;
int l = 0, r = nums.size() - 1;
while (l < r) //找到区间分界点 最小值
{
int mid = l + r >> 1;
if (nums[mid] <= nums.back()) r = mid;
else l = mid + 1;
}
if (target <= nums.back()) r = nums.size() - 1; //右半区间去找
else l = 0, r --; //左半区间去找
while (l < r)
{
int mid = l + r + 1 >> 1;
if (nums[mid] <= target) l = mid;
else r = mid - 1;
}
return nums[l] == target ? l : -1;
}
};

