题目描述

Given the array houses and an integer k. where houses[i] is the location of the ith house along a street, your task is to allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The answer is guaranteed to fit in a 32-bit signed integer.

样例

Example 1:

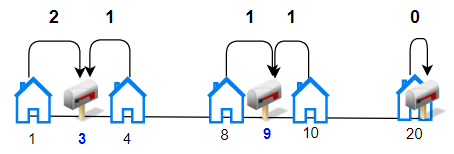
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 

Example 2:

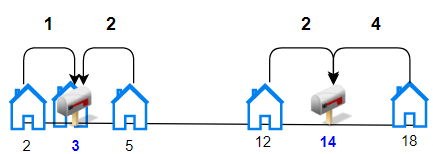
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

Example 3:

Input: houses = [7,4,6,1], k = 1
Output: 8

Example 4:

Input: houses = [3,6,14,10], k = 4
Output: 0

Constraints:

• n == houses.length
• 1 <= n <= 100
• 1 <= houses[i] <= 10^4
• 1 <= k <= n
• Array houses contain unique integers.

算法

(区间DP) $O(n^3)$

class Solution {
public:
    int minDistance(vector<int>& houses, int m) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        sort(houses.begin(), houses.end());
        int n = houses.size();
        vector<vector<int>> d(n + 1, vector<int>(m + 1, INT_MAX / 2)), f(n + 1, vector<int>(n + 1, 0));
        for (int i = 1; i < n; ++i) {
            for (int j = i + 1; j <= n; ++j) {
                f[i][j] = f[i][j - 1] + houses[j - 1] - houses[((i + j) >> 1) - 1];
            }
        }

        for (int i = 1; i <= n; ++i) d[i][1] = f[1][i];

        for (int i = 1; i <= n; ++i) {
            for (int j = 2; j <= i && j <= m; ++j) {
                for (int k = j - 1; k < i; ++k) {
                    d[i][j] = min(d[i][j], d[k][j - 1] + f[k + 1][i]);
                }
            }
        }

        return d[n][m];
    }
};

很典型的区间DP，原型是洛谷-P4677 山区建小学，时间复杂度$O(n^3)$。

用d[i][j]代表前i个房子建立j个邮筒的最小距离总和，f[i][j]代表从第i个房子到第j个房子只建立一个邮筒的最小距离和。

f[i][j]的状态转移方程：

f[i][j] = f[i][j - 1] + houses[j - 1] - houses[((i + j) >> 1) - 1];

考虑三个房子1，2，3。那么最优选择是建立在2，当多了一个房子4，其实还是建在2，那么只是多出了4到2的距离。

如果原来是1，2，3，4。最初是建在2和3都一样，一开始肯定建在(1 + 4) / 2的位置，也就是2，现在多了一个房子5，那么最优选择是建在3，前四个的距离是没有变化的，仍然只是多出了5到3的距离，也就是上面表达式的内容。注意下标的对应关系。

d[i][j]的状态转移方程：

d[i][j] = min(d[i][j], d[k][j - 1] + m[k + 1][i]);

表示前k个房子建立j-1个邮筒，第k+1个房子到i建立一个邮筒。