题目描述

给定一张L个点、P条边的有向图，每个点都有一个权值f[i]，每条边都有一个权值t[i]。

求图中的一个环，使“环上各点的权值之和”除以“环上各边的权值之和”最大。

输出这个最大值。

注意：数据保证至少存在一个环。
输入格式

第一行包含两个整数L和P。

接下来L行每行一个整数，表示f[i]。

再接下来P行，每行三个整数a，b，t[i]，表示点a和b之间存在一条边，边的权值为t[i]。
输出格式

输出一个数表示结果，保留两位小数。
数据范围

2≤L≤1000,
2≤P≤5000,
1≤f[i],t[i]≤1000

样例

输入样例：

5 7
30
10
10
5
10
1 2 3
2 3 2
3 4 5
3 5 2
4 5 5
5 1 3
5 2 2

输出样例：

6.00

题意：有向图，每条边每个点都有权值，求一个环，使环上各点的权值之和比上各边的权值之和最大

01分数规划：
边权和点权数据范围最大到1000，所以比值的范围应为(0,1000]，对于区间进行二分，如果得到某个环的比值比mid大，那么继续在右半边区间二分。

那么如何判断呢？
令当前二分的值为mid（比值不好打，放上课截图）
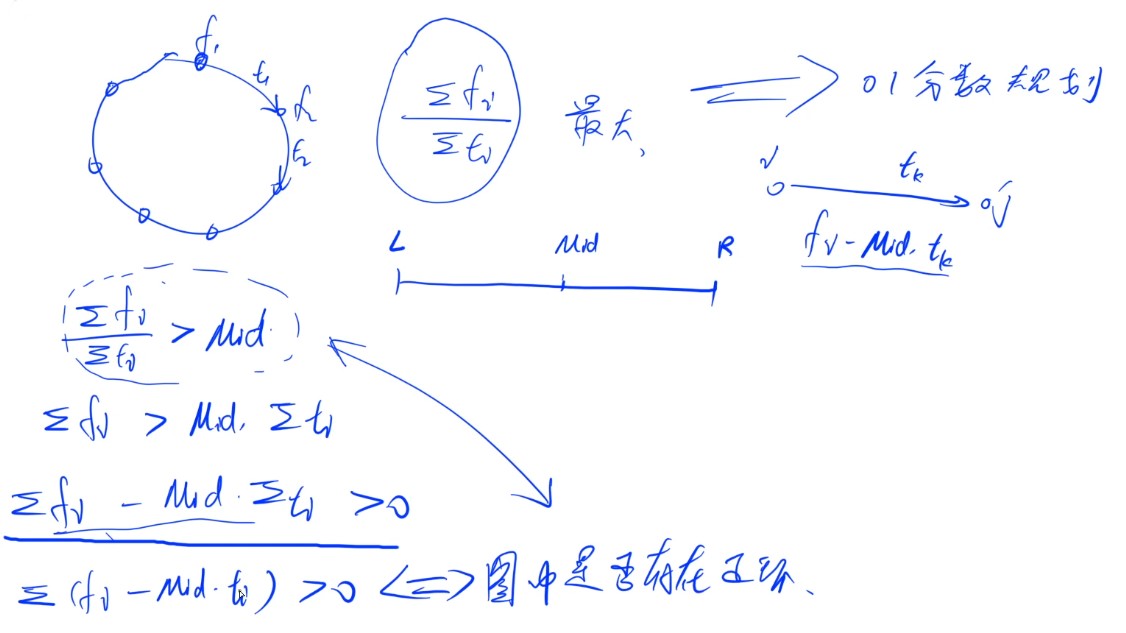那么最后就转化为了是否有正环的问题（有正环不等于没有负环哦，所以不能用是否有负环来判断）
判断是否有正环的方法和判断负环的方法是一样的，依旧是抽屉原理，如果某两个点之间的最长路的边数>=n，那么就是有正环。在代码方面和求负环也只是大小号变化。

C++ 代码

#include<iostream>
#include<cstring>
using namespace std;

const int N=1010,M=5010;

int wp[N];
int h[N],e[M],ne[M],wl[M],idx;
int n,m;
int cnt[N],st[N],q[N];
double dist[N];

void add(int a,int b,int c){
    e[idx]=b,ne[idx]=h[a],wl[idx]=c,h[a]=idx++;
}
bool check(double mid){
    memset(dist,0,sizeof dist);
    memset(cnt,0,sizeof cnt);
    memset(st,0,sizeof st);
    int hh=0,tt=0;
    for(int i=1;i<=n;i++){
        q[tt++]=i;
        st[i]=1;
    }
    while(hh!=tt){
        int t=q[hh++];
        if(hh==N)   hh=0;
        st[t]=0;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(dist[j]<dist[t]+wp[t]-mid*wl[i]){
                dist[j]=dist[t]+wp[t]-mid*wl[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>=n)   return true;
                if(!st[j]){
                    q[tt++]=j;
                    if(tt==N)   tt=0;
                    st[j]=1;
                }
            }
        }
    }
    return false;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)    cin>>wp[i];
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    double l=0,r=1010;
    while(r-l>1e-4){
        double mid=(r+l)/2;
        if(check(mid))  l=mid;
        else    r=mid;
    }
    printf("%.2lf",l);
    return 0;
}