题目描述

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

请你设计并实现 getKthAncestor(int node, int k) 函数，函数返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回-1 。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

示例：

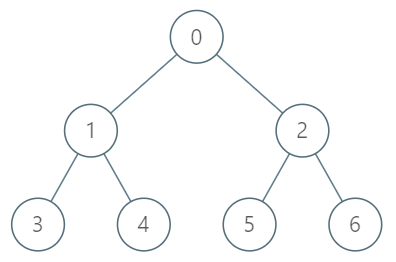
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

输出：
[null,1,0,-1]

解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

提示：

• $1 <= k <= n <= 5*10^4$
• $parent[0] == -1$ 表示编号为 $0$ 的节点是根节点。
• 对于所有的 $0 < i < n ，0 <= parent[i] < n$ 总成立
• $0 <= node < n$
• 至多查询 $5*10^4$ 次

算法思路

倍增

最多有$5*10^4$ 个结点，最坏情况下所有结点连成一条链，由于查询次数也是指数级别，如果一个结点一个结点地往上找祖先，必然会超时。所以我们可以利用倍增的思想，用数组f表示每个结点能够跳到的祖先节点。其中f[x][k]表示结点x往上跳$2^k$步后能够到达的祖先节点。

又由于
$2^{16} = 65536 > 5\*10^4， 2^{15} = 32768 < 5\*10^4$
所以$5*10^4$二进制表示最多有16位，因此最坏情况下我们利用f[x][0] ~ f[x][15]一定能跳到x的祖先节点。
$2^0 + 2^1 + … + 2^{15} = 2^{16} - 1$,所以我们数组f的第二维可以取为16.

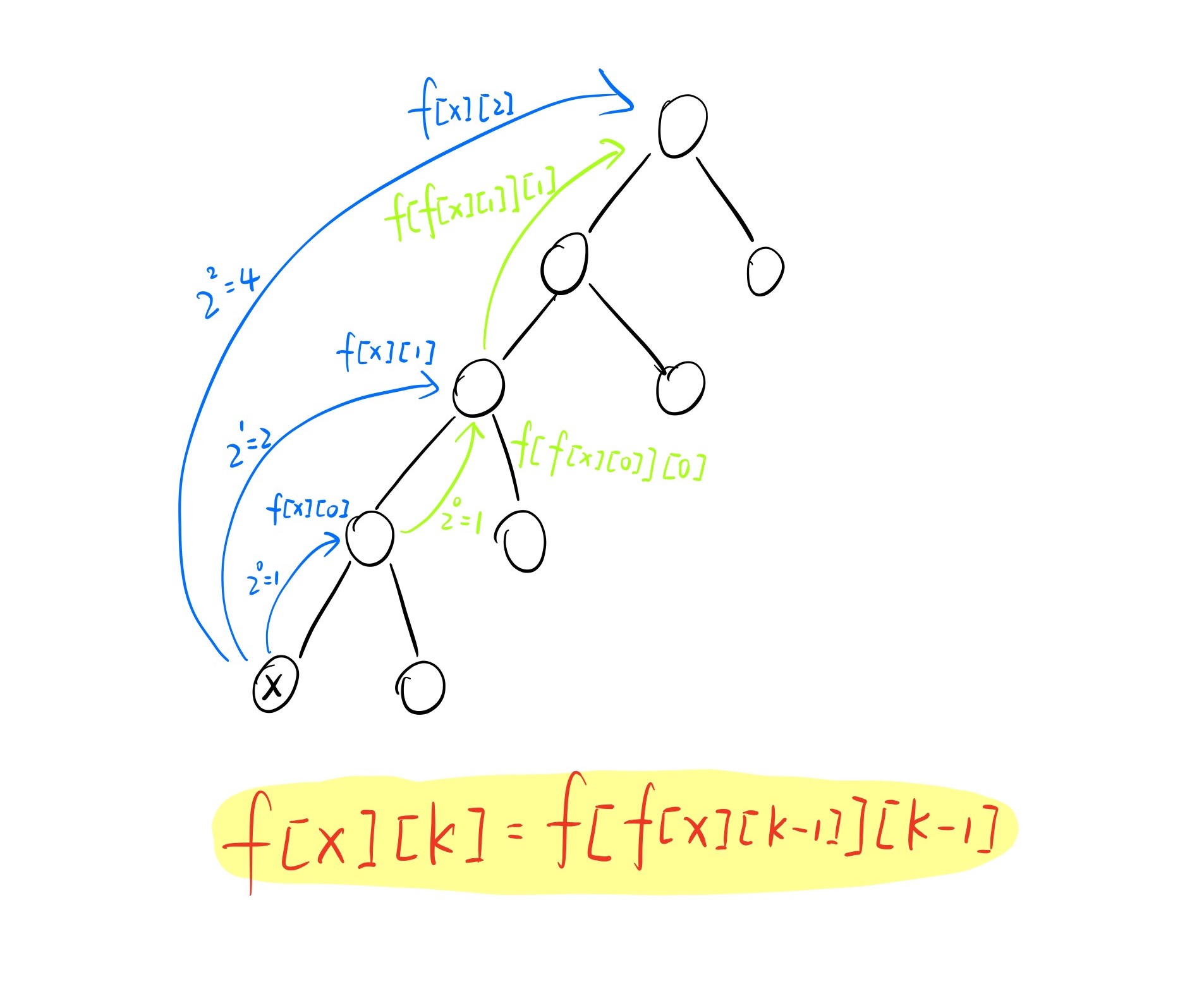
由下图可得递推式f[x][k] = f[f[x][k - 1]][k - 1]，所以先利用递推式对f数组进行预处理，当我们需要找到第k个祖先时，将k分解成2的次方之和，分步往上跳。

由于f[x][k]中计算关于点x的祖先信息时，需要用到f[x][k - 1]的信息，而f[x][k - 1]在点x的上方，因此我们预处理f数组时应该从上往下处理，由于dfs可能爆栈，所以可以采用bfs进行更新。

C ++代码

class TreeAncestor {
public:
    vector<vector<int>> f;
    vector<vector<int>> g;
    TreeAncestor(int n, vector<int>& p) {
        f = vector<vector<int>> (n, vector<int> (16, -1));
        g = vector<vector<int>> (n);

        int root = 0;
        for (int i = 0; i < n; i ++)
        {
            if (p[i] == -1) root = i;
            else g[p[i]].push_back(i);
        }

        queue<int> q;
        q.push(root);

        while (q.size())
        {
            auto t = q.front();
            q.pop();

            for (auto &x : g[t])
            {
                f[x][0] = t;
                for (int k = 1; k < 16; k ++)
                    if (f[x][k - 1] != -1) //还没到头
                        f[x][k] = f[f[x][k - 1]][k - 1];
                q.push(x);
            }
        }
    }

    int getKthAncestor(int node, int k) {
        for (int i = 0; i < 16; i ++) //将k看成二进制数
            if (k >> i & 1) 
            {
                node = f[node][i];
                if (node == -1) return node; //到头了
            }
        return node;
    }
};

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor* obj = new TreeAncestor(n, parent);
 * int param_1 = obj->getKthAncestor(node,k);
 */