题目描述

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

请你设计并实现 getKthAncestor(int node, int k) 函数，函数返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

样例

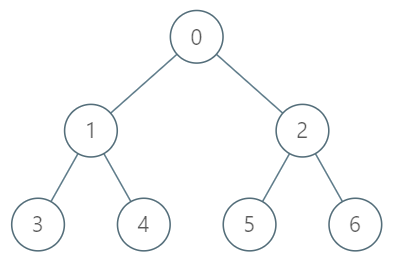
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

输出：
[null,1,0,-1]

解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

限制

• $1 \leq k \leq n \leq 5*10^4$
• $parent[0] = -1 表示编号为 0 的节点是根节点。$
• $对于所有的 0 < i < n ，0 \leq parent[i] < n 总成立$
• $0 \leq node < n$
• $至多查询 5*10^4 次$

算法

(倍增) $O(mlog(n))$

1. 设$f[i][j]$表示从点$i$向上跳$2^j$次能到达的点
2. 状态转移：先向上跳$2^{j-1}$次，再从该位置向上跳$2^{j-1}$次
   $f[i][j] = f[f[i][j - 1]][j - 1]$
3. 最坏情况下是一个长度为$5*10^4$的链表，因此$f$的第二个维度设为16足够
4. 初始时，从根节点向下用$BFS$预处理出$f$的值

时间复杂度

1. 初始化时，宽搜每个节点都会被枚举到，并且更新$f$的状态，时间复杂度为$O(n * 16)$
2. 查询时，设查询$m$次，每次查询复杂度为$O(log(n))$，因此总时间复杂度为$O(mlog(n))$

C++ 代码

class TreeAncestor {
public:
    vector<vector<int>> f, g;
    int root;

    TreeAncestor(int n, vector<int>& p) {
        f = vector<vector<int>>(n, vector<int>(16, -1));
        g = vector<vector<int>>(n);

        for (int i = 0; i < p.size(); i ++ )
            if (p[i] == -1) root = i;
            else g[p[i]].push_back(i);

        queue<int> q; q.push(root);

        while (q.size()) {
            int t = q.front(); q.pop();
            for (auto c : g[t]) {
                q.push(c);
                f[c][0] = t;
                for (int k = 1; k < 16; k ++ )
                    if (f[c][k - 1] != -1)
                        f[c][k] = f[f[c][k - 1]][k - 1];
            }
        }
    }

    int getKthAncestor(int node, int k) {
        for (int i = 16; i >= 0; i -- )
            if (k >> i & 1) {
                node = f[node][i];
                if (node == -1) return -1;
            }
        return node;
    }
};

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor* obj = new TreeAncestor(n, parent);
 * int param_1 = obj->getKthAncestor(node,k);
 */