题目描述

给定一个房屋数组 houses 和一个整数 k，其中 houses[i] 是第 i 栋房子在一条街上的位置，现需要在这条街上安排 k 个邮筒。

请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。

答案保证在 32 位有符号整数范围以内。

样例

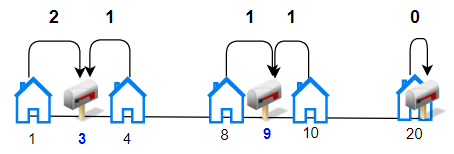
输入：houses = [1,4,8,10,20], k = 3
输出：5
解释：将邮筒分别安放在位置 3， 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5。

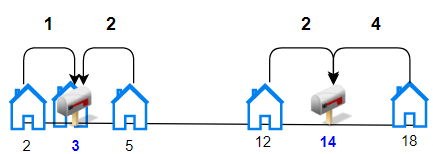
输入：houses = [2,3,5,12,18], k = 2
输出：9
解释：将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9。

输入：houses = [7,4,6,1], k = 1
输出：8

输入：houses = [3,6,14,10], k = 4
输出：0

限制

• n == houses.length
• 1 <= n <= 100
• 1 <= houses[i] <= 10^4
• 1 <= k <= n
• 数组 houses 中的整数互不相同。

算法

(贪心，动态规划) $O(n^2(n+k))$

1. 首先将房屋坐标从小到大排序。预处理 cost 数组，$cost(i, j)$ 表示闭区间 [i, j] 中的所有房屋使用同一个邮筒需要的总距离。这一步可以贪心得到，最优的邮筒必定是位于所有房屋中位数的位置（如果房屋数量为偶数则位于中间两个房屋之间的任意位置）。最优时，计算需要像回文一样配对累加距离。
2. 设状态 $f(i, j)$ 表示前 $i$ 个房屋，分为 $j$ 段的最小总距离。这里的一段表示这一段连续的房屋用同一个邮筒，因为最优解一定是连续的一段房屋用同一个邮筒，再连续的一段用下一个邮筒。有效房屋的下标从 1 开始。
3. 初始时，$f(0, 0) = 0$，其余为正无穷。
4. 转移时，对于 $i$ 和 $j$，枚举当前段的起点 $l$，令闭区间 [l, i] 使用同一个邮筒，则转移 $f(i, j) = \min(f(l - 1, j - 1) + cost(l, i))$。
5. 最终答案为 $f(n, k)$。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。预处理的时间复杂度为 $O(n^3)$。
• 动态规划状态数为 $O(nk)$，每次有 $O(n)$ 种转移。
• 总时间复杂度为 $O(n^2(n + k))$。

空间复杂度

• 需要额外 $O(n(n + k))$ 的空间存储 cost 数组和动态规划的状态。

C++ 代码

class Solution {
public:
    int calc(const vector<int> &houses, int l, int r) {
        int tot = 0;
        for (; l < r; l++, r--)
            tot += houses[r] - houses[l];

        return tot;
    }

    int minDistance(vector<int>& houses, int k) {
        const int INF = 1000000000;
        int n = houses.size();
        sort(houses.begin(), houses.end());

        vector<vector<int>> cost(n + 1, vector<int>(n + 1));

        for (int i = 1; i <= n; i++)
            for (int j = i; j <= n; j++)
                cost[i][j] = calc(houses, i - 1, j - 1);

        vector<vector<int>> f(n + 1, vector<int>(k + 1, INF));

        f[0][0] = 0;

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= k; j++)
                for (int l = i; l >= 1; l--)
                    f[i][j] = min(f[i][j], f[l - 1][j - 1] + cost[l][i]);

        return f[n][k];
    }
};