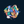题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

样例

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

算法1

(暴力枚举) $O(n^2)$

对于数组中的每个元素，找出下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值。

C++ 代码

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        int n = height.size();

        for (int i = 1; i < n; i ++)
        {
            int l = 0, r = 0;
            for (int j = i; j >= 0; j --)
            l = max(l, height[j]);

            for (int j = i; j < n; j ++)
            r = max(r, height[j]);

            ans += min(l, r) - height[i];
        }

        return ans;
    }
};

算法2

(前缀和思想) $O(n)$

可以利用前缀和思想预处理每个点左侧以及右侧的最大值，将时间复杂度降到O(n)

C++ 代码

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        int n = height.size();
        if (n == 0) return 0;
        vector<int> l(n), r(n);

        //求该点左侧最高点
        l[0] = height[0];
        for (int i = 1; i < n; i ++)
        l[i] = max(height[i], l[i - 1]);

        //求该店右侧最高点
        r[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i --)
        r[i] = max(height[i], r[i + 1]);

        for (int i = 1; i < n - 1; i ++)
        ans += min(l[i], r[i]) - height[i];

        return ans;
    }
};