算法

(带权并查集) $O(n)$

题目大意：有一个数列长度为$n$，然后给出$m$个描述，每个给出一个区间上的和，要求这$m$个描述中有多少个是会和前面的描述冲突的。

题解：对于这个题目，我们是不知道数列的具体内容的，只知道若干区间上的和是多少，然而如果区间是相邻的，那么他们可以组合成一个更大的区间，也就是通过已有区间能推理出更多的区间和。这道题使用带权并查集的做法很好处理，每一个结点表示一个区间的起点，它的父亲结点表示这个左闭右开区间的右端点，边上的权值就存这个左闭右开区间上的和。对于给出的每一个描述，都判断是否连通，如果是，就判断给出的数据和推得的数据是否吻合，如果不连通，就通过并查集的合并操作使其连通。

模拟一下样例：

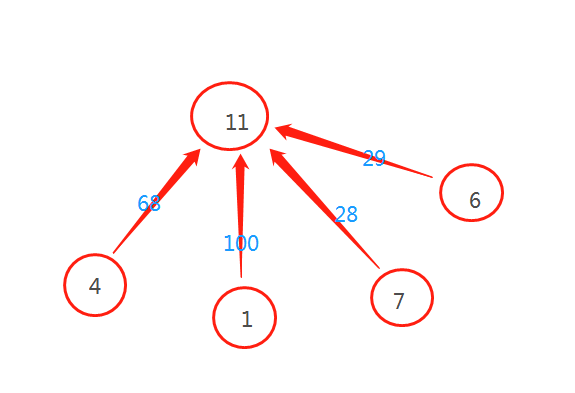
这里$[4, 7)$的区间和应该为$40$，而不是$41$。

C++ 代码

#include <iostream>

using namespace std;

const int N = 2e5 + 10;

int n, m, ans;
int p[N], val[N];

// 并查集核心操作
int find(int x) {
    if (p[x] == x) return x;
    int new_p = find(p[x]);
    // 这道题的权值是累加的，因此当前边权要加上父亲节点到根节点的和 
    val[x] += val[p[x]]; 
    p[x] = new_p; // 路径压缩 
    return p[x];
} 

int main() {
    ios::sync_with_stdio(0);
    while (cin >> n >> m) {
        ans = 0;
        for (int i = 0; i <= n + 1; ++i) // 0要初始化，数据中好像用到了 
            p[i] = i, val[i] = 0;
        for (int i = 1, a, b, s; i <= m; ++i) {
            cin >> a >> b >> s;
            if (find(a) == find(++b))
                ans += val[a] != val[b] + s; // 判断给的数据是否吻合 
            else { // 连通两个块 
                val[p[a]] = val[b] + s - val[a]; // 由带权并查集的四边形原理得到 
                p[p[a]] = p[b]; // 此题中的边权可以是负数，代表从后往前的一个反向区间，能避免正负等的分类讨论 
            }
        }
        cout << ans << '\n';
    }
    return 0;
}