题目描述

给你一个房屋数组houses 和一个整数 k ，其中 houses[i] 是第 i 栋房子在一条街上的位置，现需要在这条街上安排 k 个邮筒。

请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。

答案保证在 32 位有符号整数范围以内。

样例

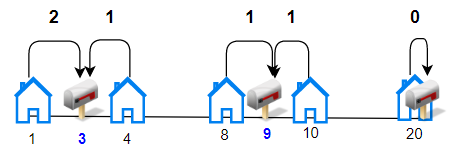
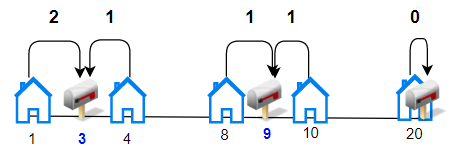
输入：houses = [1,4,8,10,20], k = 3
输出：5
解释：将邮筒分别安放在位置 3， 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。

输入：houses = [2,3,5,12,18], k = 2
输出：9
解释：将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。

输入：houses = [7,4,6,1], k = 1
输出：8

输入：houses = [3,6,14,10], k = 4
输出：0

算法分析

最优解的特殊性：所有邮筒都落在房子上必有最优解的情况

对于某种方案，假设有一个邮筒没有房子，且左边有L个房子离它最近，有右边R个房子离它最近，根据 Acwing 104. 货仓选址 题可知，如果L >= R，邮筒往左边移动，总距离不会变大，如果L < R，邮筒往右边移动，总距离不会变大，因此可知落在中间的房子上总距离一定是最小。因此最优解中一定存在所有邮筒都放在房子中的情况

操作

• 1、先预处理a[i][j],表示在[i,j]区间中，放一个邮筒的总的最短距离
• 2、如图所示

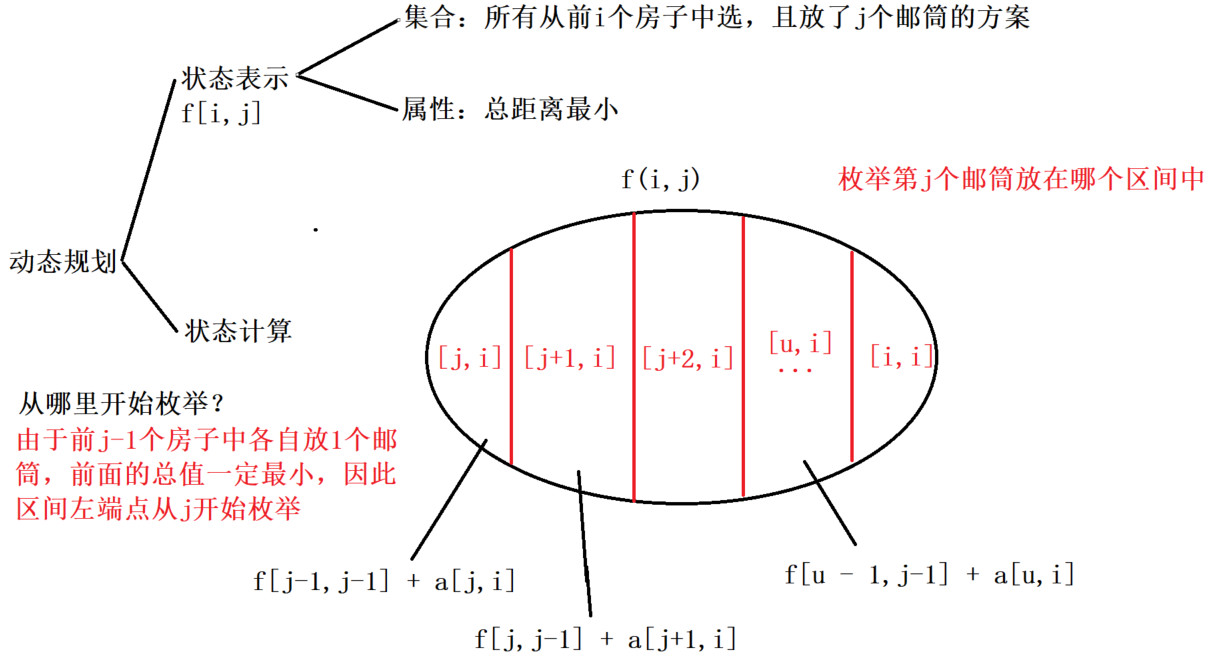
• 3、初始化：从前i个房子中，当只放一个邮筒的总的最短距离f[i][1] = a[1][i]，其余初始化为正无穷大
• 4、结果：f[n,k]
• 5、为了思路清晰，坐标从1开始

时间复杂度 $O(n^2(n + k))$

Java 代码

class Solution {
    static int N = 110;
    static int INF = 0x3f3f3f3f;
    public int minDistance(int[] houses, int k) {
        int n = houses.length;
        int[] house = new int[n + 1];
        for(int i = 1;i <= n;i ++) house[i] = houses[i - 1];
        Arrays.sort(house,1,n + 1);
        int[][] a = new int[N][N];
        //计算出从i到j中用一个邮筒所需要的最小代价
        for(int i = 1;i <= n;i ++)
            for(int j = i;j <= n;j ++)
            {
                int mid = i + j >> 1;
                int t = 0;
                for(int u = i;u <= j;u ++)
                {
                    t += Math.abs(house[u] - house[mid]);
                }
                a[i][j] = t;
            }
        int[][] f = new int[N][N];
        for(int i = 0;i <= n;i ++)
            Arrays.fill(f[i],INF);

        for(int i = 1;i <= n;i ++) f[i][1] = a[1][i];
        for(int i = 1;i <= n;i ++)
        {
            for(int j = 2;j <= k && j <= i;j ++)
            {
                for(int u = j;u <= i;u ++)
                {
                    f[i][j] = Math.min(f[i][j],f[u - 1][j - 1] + a[u][i]);
                }
            }
        }
        return f[n][k];
    }
}