题目描述

给定一个整数数组，你需要寻找一个连续的子数组，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

你找到的子数组应是最短的，请输出它的长度。

说明 :

输入的数组长度范围在[1, 10,000]。
输入的数组可能包含重复元素 ，所以升序的意思是<=。

样例

输入:
[2, 6, 4, 8, 10, 9, 15]

输出: 
5

解释:
你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

算法1

(线性遍历) $O(n)$

遍历过程中 ：

• 找到 从左到右 最后一个 破坏递增性质的数的下标 —— left
• 找到 从右到左 最后一个 破坏递减性质的数的小标 —— right

如何判断其破坏了递增或者递减性质

破坏递增 ： 当前数小于 前缀中的最大值 - max_v
破坏递减 ： 当前数大于 后缀中的最小值 - min_v

所以还需要维护一个前缀中的最大值以及后缀中的最小值

C++ 代码

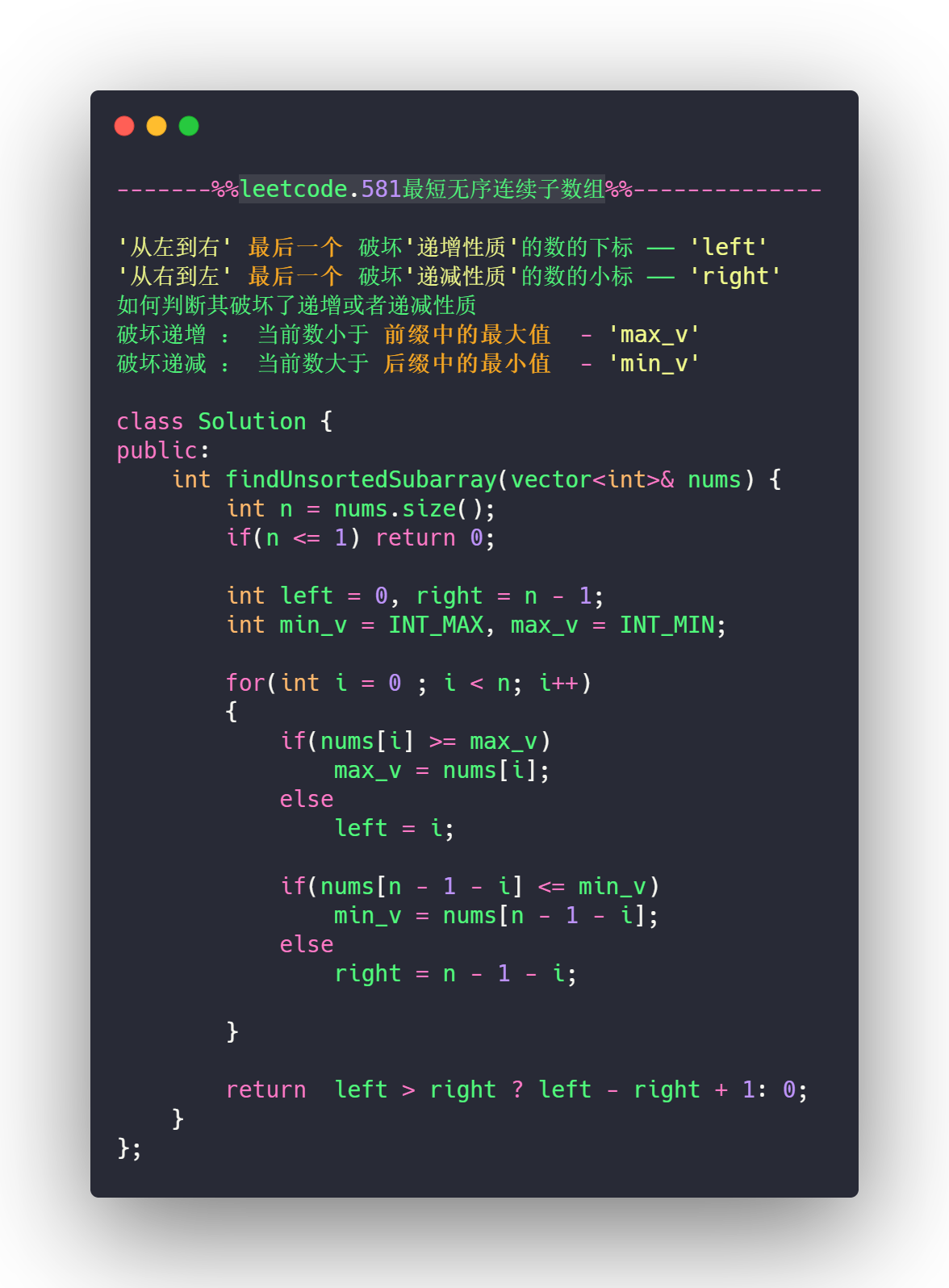
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int n = nums.size();
        if(n <= 1) return 0;
        //从左到右最后一个 破坏递增性质的数的下标 —— left
        //从右到左最后一个 破坏递减性质的数的小标 —— right
        int left = 0, right = n - 1;
        // 如何判断其破坏了递增或者递减性质
        // 破坏递增 ： 当前数小于 前缀中的最大值
        // 破坏递减 ： 当前数大于 后缀中的最小值
        int min_v = INT_MAX, max_v = INT_MIN;

        for(int i = 0 ; i < n; i++)
        {
            if(nums[i] >= max_v)
                max_v = nums[i];
            else
                left = i;

            if(nums[n - 1 - i] <= min_v)
                min_v = nums[n - 1 - i];
            else
                right = n - 1 - i;

        }

        return  left > right ? left - right + 1: 0;
    }
};