题目描述

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

样例

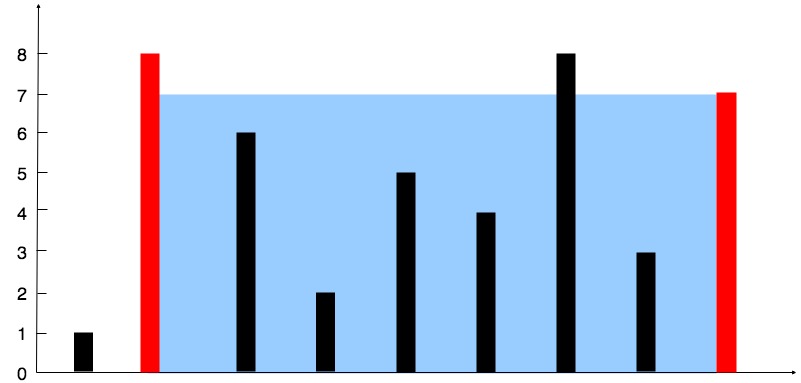
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

输入：[1,8,6,2,5,4,8,3,7]
输出：49

算法分析

贪心 + 双指针

思路很难，操作简单

操作

• 1、l指针维护左边界，r指针维护右边界，l和r维护的是当前容器的大小，即min(l,r) * (r - l)
• 2、若height[l] < height[r],l向右移动，若height[l] >= height[r]，r向左移动，更新移动后的容器大小res

证明

LeetCode官方证明的搬运工，解释清晰

为什么双指针的做法是正确的？

1、双指针代表了什么？

双指针代表的是 可以作为容器边界的所有位置的范围。在一开始，双指针指向数组的左右边界，表示 数组中所有的位置都可以作为容器的边界，因为我们还没有进行过任何尝试。在这之后，我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置，就表示我们认为 这个指针不可能再作为容器的边界了。

2、为什么对应的数字较小的那个指针不可能再作为容器的边界了？

在上面的分析部分，我们对这个问题有了一点初步的想法。这里我们定量地进行证明。

考虑第一步，假设当前左指针和右指针指向的数分别为 $x$ 和 $y$，不失一般性，我们假设 $x <= y$。同时，两个指针之间的距离为 $t$。那么，它们组成的容器的容量为：$min(x,y)∗t=x∗t$

我们可以断定，如果我们保持左指针的位置不变，那么无论右指针在哪里，这个容器的容量都不会超过 $x * t$ 了。注意这里右指针只能向左移动，因为 我们考虑的是第一步，也就是 指针还指向数组的左右边界的时候。

我们任意向左移动右指针，指向的数为 $y_1$，两个指针之间的距离为$t_1$，那么显然有$t_1 < t$，并且$min(x,y_1) <= min(x,y)$

• 如果$y_1 <= y$ ，那么$min(x,y_1) <= min(x,y)$
• 如果$y_1 > y$，那么$min(x,y_1) = x = min(x,y)$

因此有 $min(x,y_t) * t_1 <= min(x,y) * t$

即无论我们怎么移动右指针，得到的容器的容量都小于移动前容器的容量。也就是说，这个左指针对应的数不会作为容器的边界了，那么我们就可以丢弃这个位置，将左指针向右移动一个位置，此时新的左指针于原先的右指针之间的左右位置，才可能会作为容器的边界。

这样以来，我们将问题的规模减小了 $1$，被我们丢弃的那个位置就相当于消失了。此时的左右指针，就指向了一个新的、规模减少了的问题的数组的左右边界，因此，我们可以继续像之前 考虑第一步 那样考虑这个问题：

• 求出当前双指针对应的容器的容量；

• 对应数字较小的那个指针以后不可能作为容器的边界了，将其丢弃，并移动对应的指针。

最后的答案是什么？

答案就是我们每次以双指针为左右边界（也就是「数组」的左右边界）计算出的容量中的最大值。

链接： 官方解释

时间复杂度 $O(n)$

Java 代码

class Solution {
    public int maxArea(int[] height) {
        int n = height.length;
        int l = 0,r = n - 1;
        int res = 0;
        while(l < r)
        {
            res = Math.max(res,Math.min(height[l],height[r]) * (r - l));
            if(height[l] < height[r]) l ++;
            else r --;
        }
        return res;
    }
}