要点；

1.**如何确定每个物品选与不选**

1.1:对于从1到n得到的拓扑图，f[n][m]是终点，f[i][j]的意思是从前i个物品中，体积不超过j的max

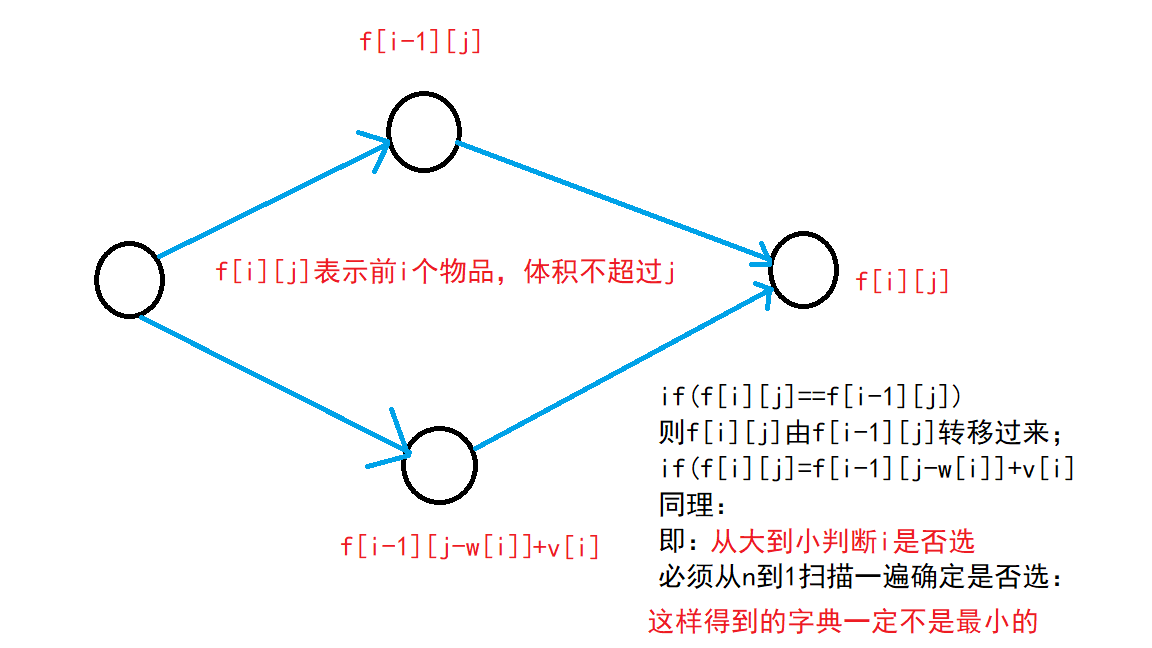
1.2: 对于从n到1得到的拓扑图，f[1][m]是终点，f[i][j]的意思是第i个物品到最后一个物品中选，体积不超过j的max

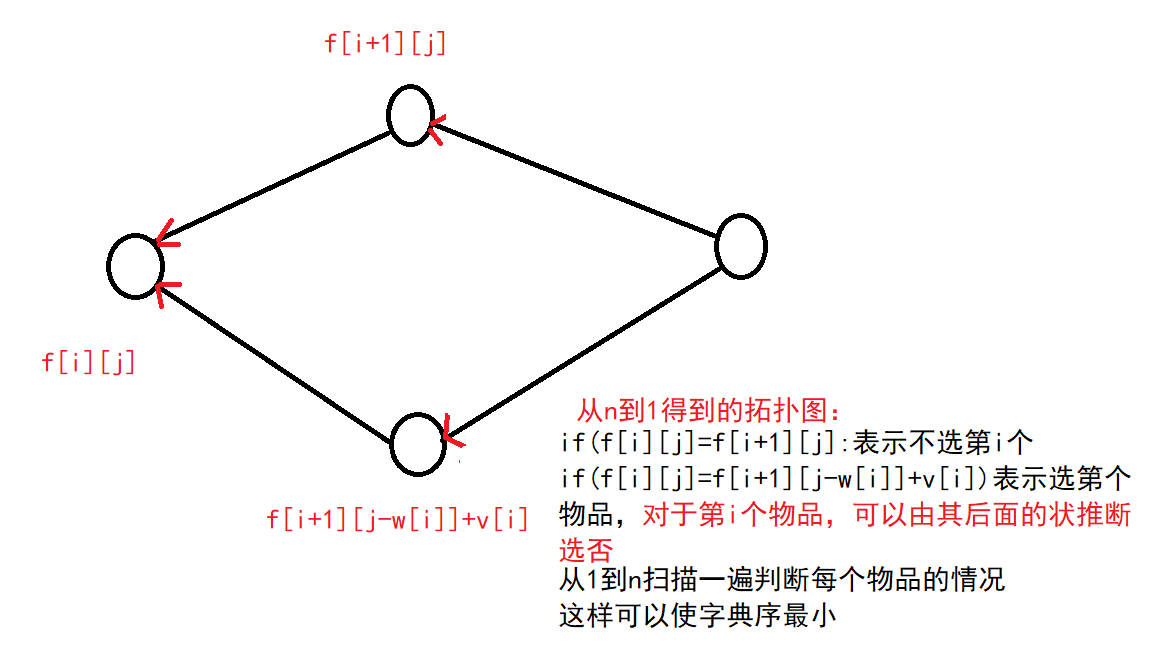
2.**如何确定每个物品的情况使字典序最小**

对于每个物品都有三中情况：
  必须选
  必须不选
  可选可不选(在1.2中，从小到大遍历i时，遇到这种情况一定选可以使字典序最小)

上代码

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int w[N],v[N];
int f[N][N];
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    scanf("%d%d",&w[i],&v[i]);
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        { 
            f[i][j]=f[i+1][j];

            if(j>=w[i]) f[i][j]=max(f[i][j],f[i+1][j-w[i]]+v[i]);
        }
    }
    int j=m;
    for(int i=1;i<=n;i++)
    {
        if(j>=w[i]&&f[i][j]==f[i+1][j-w[i]]+v[i])//可以选则必选,注意防止越界
        {
            cout<<i<<" ";
            j-=w[i];
        }
    }
    cout<<endl;
    return 0;
}