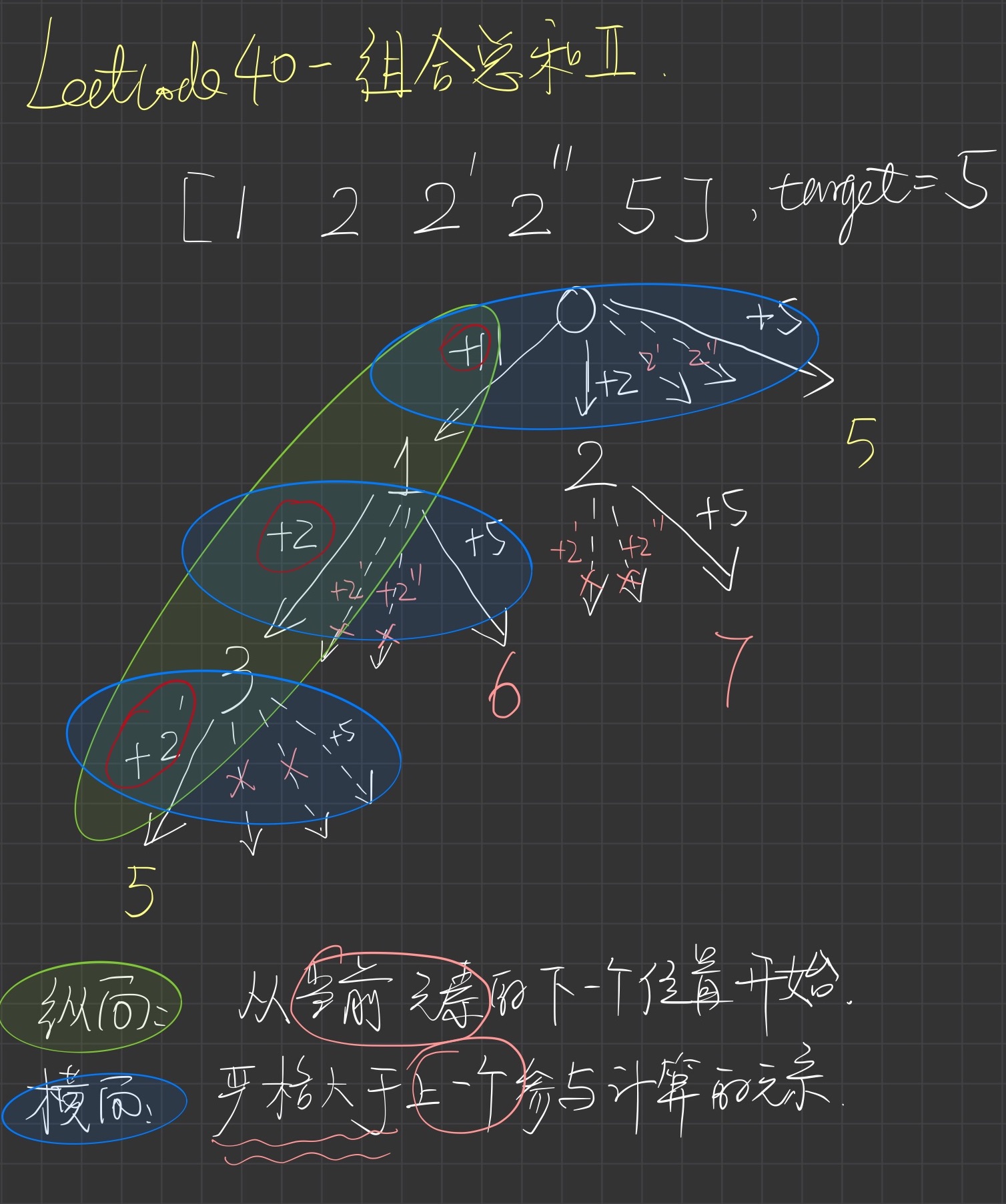
图解

代码

class Solution {
    public List<List<Integer>> combinationSum2(int[] c, int target) {
        Arrays.sort(c);
        List<List<Integer>> res = new ArrayList();
        List<Integer> path = new ArrayList();
        dfs(c, 0, 0, target, res, path);
        return res;
    }

    public void dfs(int[] c, int start, int sum, int target, List<List<Integer>> res, List<Integer> path){
        if(target == sum){
            res.add(new ArrayList(path));
            return;
        }

        for(int i = start; i < c.length; i++){
            // 纵向剪枝，当上层通路上的和加上本层元素>target时, 整颗子树生成结束
            if(sum + c[i] > target) return;
            // 横向剪枝, 当当前元素<=前一个元素时,剪枝
            if(i != start && c[i] <= c[i-1]) continue;
            path.add(c[i]);
            dfs(c, i+1, sum+c[i], target, res, path);
            path.remove(new Integer(c[i]));
        }
    }
}

dfs二刷20200711

class Solution {
    List<List<Integer>> res = new ArrayList();
    Stack<Integer> path = new Stack();

    public List<List<Integer>> combinationSum2(int[] c, int target) {
        //排序, 保证剪枝逻辑
        Arrays.sort(c);
        //参数2: 表示c中的第i位; 参数3: 剩余目标值
        dfs(c, 0, target, path);
        return res;
    }

    public void dfs(int[] c, int u, int target, Stack<Integer> path){
        if(target == 0){
            res.add(new ArrayList(path));
            return;
        }
        if(target < 0) return;

        //遍历数组, 从u开始.
        for(int i = u; i < c.length; i++){
            //剪枝逻辑是遍历过的方案路过即可
            if(i > u && c[i] == c[i-1]) continue;
            path.push(c[i]);
            dfs(c, i+1, target - c[i], path);
            path.pop();
        }
    }
}