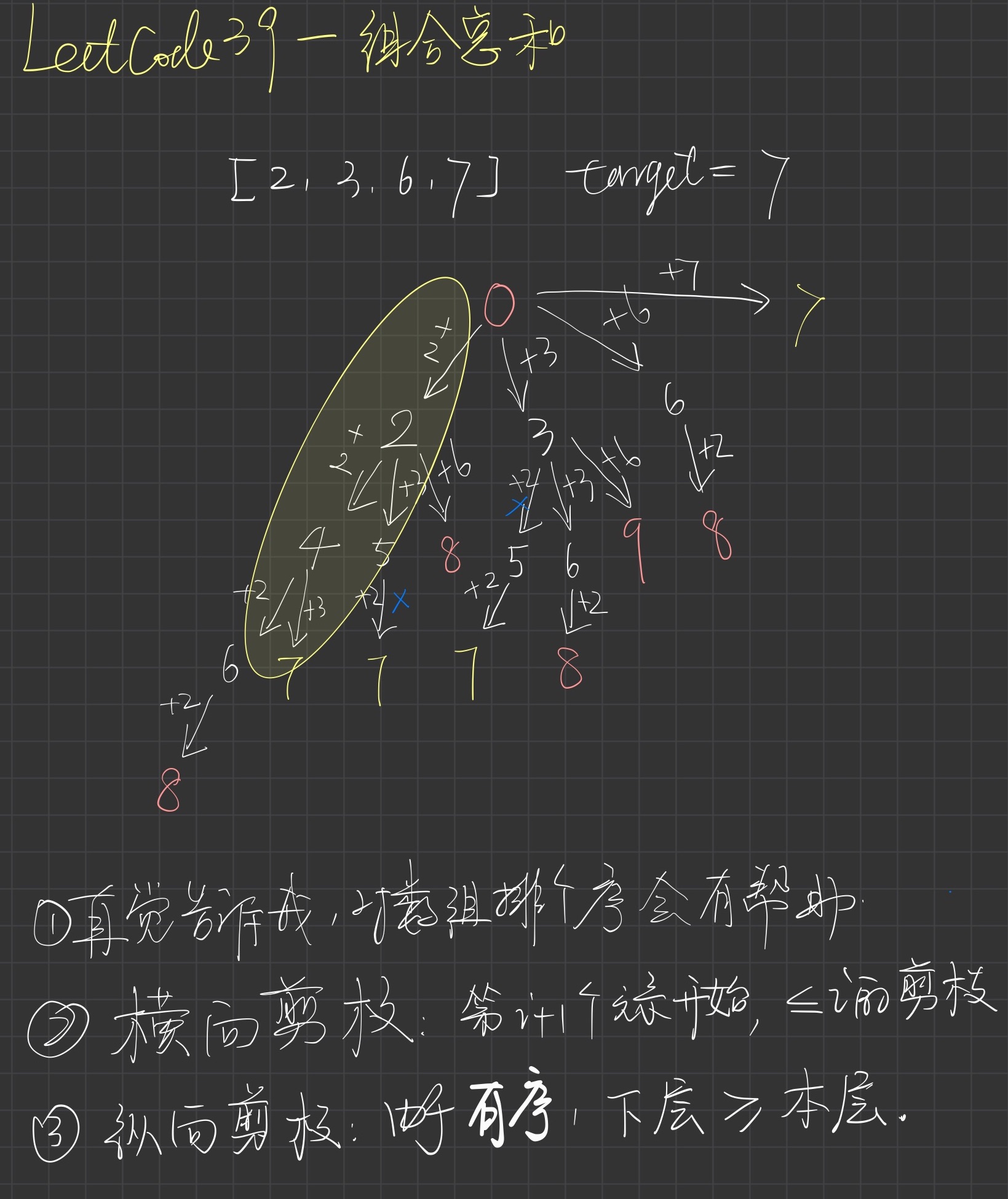
图解
深度遍历往往需要剪枝, 剪枝时确定好横向策略和纵向策略后,代码层实现就简单了。
确认横向与纵向策略的方法,需要简单画一下整棵树.
代码
class Solution {
public List<List<Integer>> combinationSum(int[] c, int target) {
List<List<Integer>> res = new ArrayList();
List<Integer> path = new ArrayList();
Arrays.sort(c);
dfs(c, 0, 0, target, res, path);
return res;
}
public void dfs(int[] c, int start, int sum, int target, List<List<Integer>> res, List<Integer> path){
if(sum == target){
res.add(new ArrayList(path));
return;
}
// 指针用来控制深度的剪枝, 小于start的点会被路过, 完成剪枝
for(int i = start; i < c.length; i++){
// 循环内部的条件用来控制横向宽度的剪枝
if(sum + c[i] > target) return;
path.add(c[i]);
dfs(c, i, sum+c[i], target, res, path);
path.remove(new Integer(c[i]));
}
}
}
二刷dfs题, 20200711
class Solution {
List<List<Integer>> res = new ArrayList();
Stack<Integer> path = new Stack();
public List<List<Integer>> combinationSum(int[] c, int target) {
dfs(c, 0, target, path);
return res;
}
public void dfs(int[] c, int u, int target, Stack<Integer> path){
if(target == 0){
res.add(new ArrayList(path));
return;
}
if(target < 0) return;
//枚举每一个数, 指针长度决定每一层的横向宽度
for(int i = u; i < c.length; i++){
path.push(c[i]);
dfs(c, i, target-c[i], path);
path.pop();
}
}
}

