在Y总的基础上，增加了图示，便于理解区间的变化。

题目描述

输入一棵二叉树前序遍历和中序遍历的结果，请重建该二叉树。

样例

给定：
前序遍历是：[3, 9, 20, 15, 7]
中序遍历是：[9, 3, 15, 20, 7]

返回：[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示：
    3
   / \
  9  20
    /  \
   15   7

算法

(递归) $O(n)$

哈希预处理，首先保存中序遍历每个节点的下标，这样方便递归每次求根节点在中序遍历时的下标。

找到了根节点在中序遍历的位置，那么左右子树的中序遍历也随之确定。

进一步的，知道的左子树的节点数量，其对应的前序遍历也确定了下来，随之右子树的前序遍历也确定。

参考文献

https://www.acwing.com/solution/content/706/

C++ 代码

// 前序 + 中序 
// 前序 -> 根节点  中序 -> 左右子树各有多少分节点
// 哈希表(unordered_map<int,int>)记录每个值在中序遍历中的位置
// 这样我们在递归到每个节点时，在中序遍历中查找根节点位置的操作，只需要O(1)

class Solution {
public:
    //快速的找到根节点的位置
    unordered_map<int, int> pos;

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for(int i = 0; i < n; i ++) pos[inorder[i]] = i;
        return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
    }

      TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir)
    {
        if (pl > pr) return NULL;
        // 当前区间【pl, pr】所表示的树的根节点  前序遍历的第一个节点就是根节点
        // 找到改区间根节点在中序遍历的位置  以及左子树的元素个数
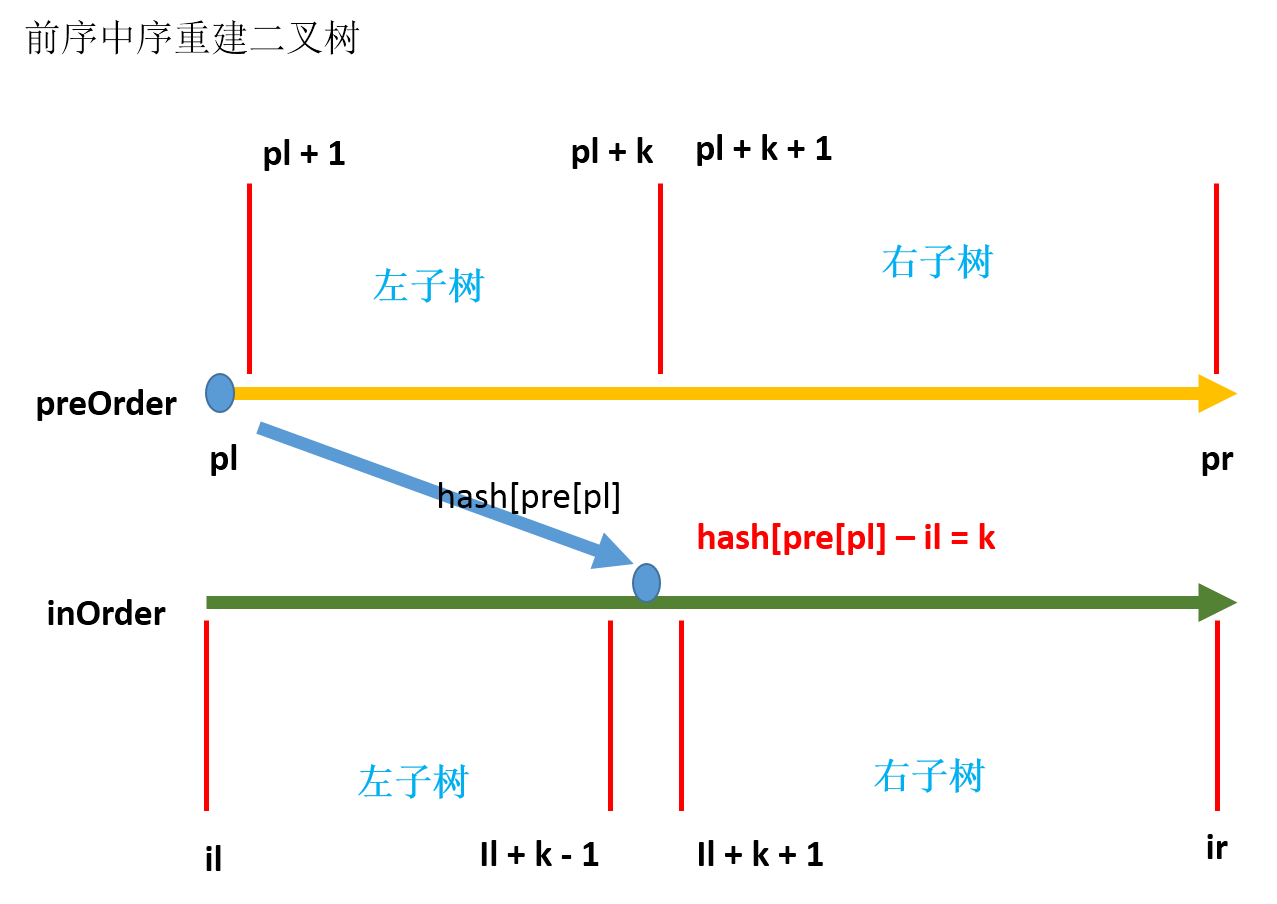
        // 左前 ：【pl + 1, pl + k】  左中【il, il + k - 1】
        // 右前 ：【pl + k + 1, pr】  右中【il + k + 1， ir】 
        int k = pos[pre[pl]] - il;  
        TreeNode* root = new TreeNode(pre[pl]);
        root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
        return root;
    }

};