题目描述
在一个3×3的网格中,1~8这8个数字和一个“x”恰好不重不漏地分布在这3×3的网格中。
例如:
1 2 3
x 4 6
7 5 8
在游戏过程中,可以把“x”与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x
例如,示例中图形就可以通过让“x”先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将3×3的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8
则输入为:1 2 3 x 4 6 7 5 8
输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出”-1”。
样例
输入样例:
2 3 4 1 5 x 7 6 8
输出样例
19
分析一下y总的思路,也相当于做个课堂笔记吧(这也太巧妙了吧,讲解视频不到20分钟,我愣是半天没想出来
1、题目的目标

求最小步数 -> 用BFS
2、移动情况
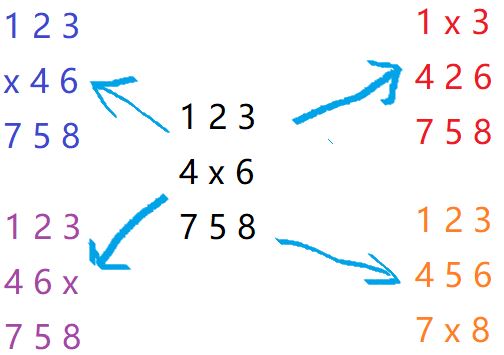
移动方式:
转以后:a = x + dx[i], b = y + dy[i].
思想:将每一种情况作为1个节点,目标情况即为终点
从初始状况移动到目标情况 —> 求最短路
3、问题
第一点:怎么表示一种情况使其能作为节点?
第二点:如何记录每一个状态的“距离”(即需要移动的次数)?
第三点:队列怎么定义,dist数组怎么定义?
4、解决方案
将 “3*3矩阵” 转化为 “字符串”
如: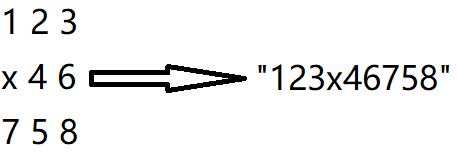
所以:
队列可以用 queue<string>
//直接存转化后的字符串
dist数组用 unordered_map<string, int>
//将字符串和数字联系在一起,字符串表示状态,数字表示距离
5、矩阵与字符串的转换方式

6、代码
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>
using namespace std;
int bfs(string start)
{
//定义目标状态
string end = "12345678x";
//定义队列和dist数组
queue<string> q;
unordered_map<string, int> d;
//初始化队列和dist数组
q.push(start);
d[start] = 0;
//转移方式
int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
while(q.size())
{
auto t = q.front();
q.pop();
//记录当前状态的距离,如果是最终状态则返回距离
int distance = d[t];
if(t == end) return distance;
//查询x在字符串中的下标,然后转换为在矩阵中的坐标
int k = t.find('x');
int x = k / 3, y = k % 3;
for(int i = 0; i < 4; i++)
{
//求转移后x的坐标
int a = x + dx[i], b = y + dy[i];
//当前坐标没有越界
if(a >= 0 && a < 3 && b >= 0 && b < 3)
{
//转移x
swap(t[k], t[a * 3 + b]);
//如果当前状态是第一次遍历,记录距离,入队
if(!d.count(t))
{
d[t] = distance + 1;
q.push(t);
}
//还原状态,为下一种转换情况做准备
swap(t[k], t[a * 3 + b]);
}
}
}
//无法转换到目标状态,返回-1
return -1;
}
int main()
{
string c, start;
//输入起始状态
for(int i = 0; i < 9; i++)
{
cin >> c;
start += c;
}
cout << bfs(start) << endl;
return 0;
}
7、参考
算法基础课:第三章:搜索与图论(一)、Week4 习题课


用string来存状态,好聪明的方法,不知道怎么存状态想了半天
牛逼 我也是 没想出来这个www
思想类似状压
我觉得可以这样来理解这种bfs,就是distance就是移动的次数,记录下来移动一遍有多少种可能,移动两遍又有多少种可能,然后一直下去,直到在产生移动第n遍时出现了我们所期望的值,那么就跳出循环,返回distance
嗯嗯这样理解好
找到一个状态的最短路径想到太妙了,矩阵压缩为一维数组也太妙了
这真的抓到bfs的精髓了
佬,能说一下您认为的精髓是啥吗
每次只增加1步的所有状态,消耗的步数都是相同的,所以谁先到达目标状态,谁就是最小值。。也许能这么解释吧
!d.count(t)为什么是代表没有搜到的状态?
d.count(t)表示t在d中出现的次数,t为没有搜到的状态的时候,d中就没有t,那它的值就是0,!0就是1谢谢
请问有人知道为什么当queue q , unordered_map d创建在bfs( )时会比 queue q , unordered_map d 创建在全局变量时的运行速度快很多,大概前者比后者能快1s算出答案。 是跟stack 和 heap 的空间有关系吗
优化了一下,不用每次find(x)
//if(!d.count(t)),这一步判断是要保证队中没有重复元素吗?
对
是判断这个字符串t是否被访问过,没有访问过才入队,访问过直接跳过
我就想问为啥用map就超时
map是红黑树自带排序,效率没unordered_map高。unordered_map是哈希表,查询是O(1)的,像这种有大量查询的问题,最好是用unordered_map。
懂了3q
unordered_map插入On,查询O1,map插入查询都是Ologn,看均摊复杂度的话还是map比较好用
//还原状态,为下一种转换情况做准备
swap(t[k], t[a * 3 + b]); 这里没懂 下一种情况咋回事
每一种状态有四种不同的转换情况(上、下、左、右),循环中需要遍历所有四种情况。这个地方是直接改变的原本状态,所以每一次循环结束要还原状态,“下一种情况“就是”上下左右“中的某一种
懂了谢谢大佬
噢噢 大佬nb~
int x = k / 3, y = k % 3;试不是写反了?不过写反是不是也不影响?
可以反着写,等价的
解释得太好了,难得一次就懂了!大佬,Orz!
太妙了
%%%
为什么不直接输入start呢?
应该是char c 吧?
都可以的其实,string c就是定义一个长度为1的字符串啊可以的! 第二个问题:为什么不直接输入start?答:因为中间有空格,可以利用cin过滤空格
为什么不能用getline
haha,重新学吧朋友,你问我为什么不用getline? 题目就是要去除空格,你用getline? 孩子你无敌了 他是存下当前的状态,用题目给的已知的状态去拓展,你能明白我的意思吗朋友?
噢噢,谢谢,新手字符串还没学。。。。
没事 我要说的是getline不能过滤空格 所以这一题不可以getline
C++输入带有空格的字符串要用到getline()
输入i k z a;实际start收到的只有i就是说i后面的空格会忽略掉
//查询x在字符串中的下标,然后转换为在矩阵中的坐标
int k = t.find(‘x’); 这一步我还是不太明白 t不是队列中出列的一个字符吗? 那t.find是怎么找到x的呢?
t是整个string字符串
大佬,为啥不能把!d.count(t)并入越界判断条件中呢?
因为此时状态还没有改变,交换后状态才改变了,这时候判断一下改变后的状态之前是否记录过
因为你要先交换之后,才知道这种情况有没有出现啊?就比如之前是s1,交换之后是s2,你需要判断的是s2有没有出现过,所以必须交换了才能判断。
强的
太妙了!