算法

(DFS)

对于这道题我们可以分为$4$种情况来讨论：

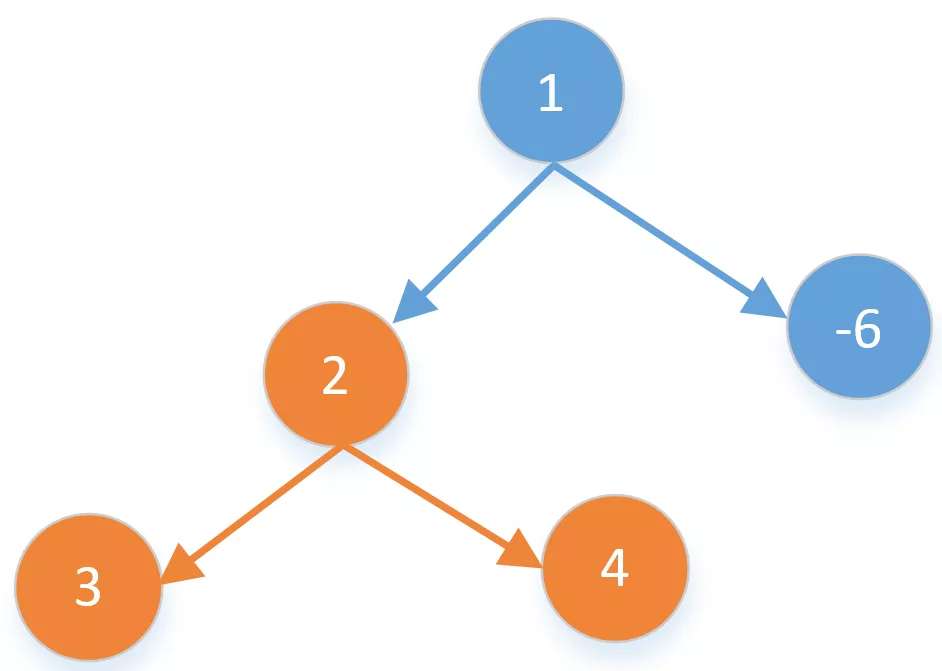
• 只要当前节点，舍弃子节点。比如下面节点为$2$的左右子节点都是负数，如果是负数我们还不如不要，所以直接舍弃子节点。
  

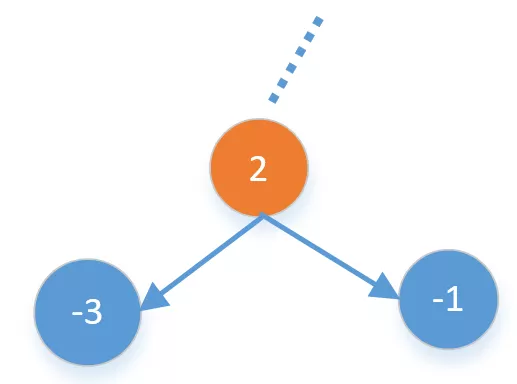
• 保留当前节点和左子节点。比如下面节点$2$的右子节点是负数，我们直接舍弃右子节点，但左子节点不是负数，我们可以保留左子节点。
  

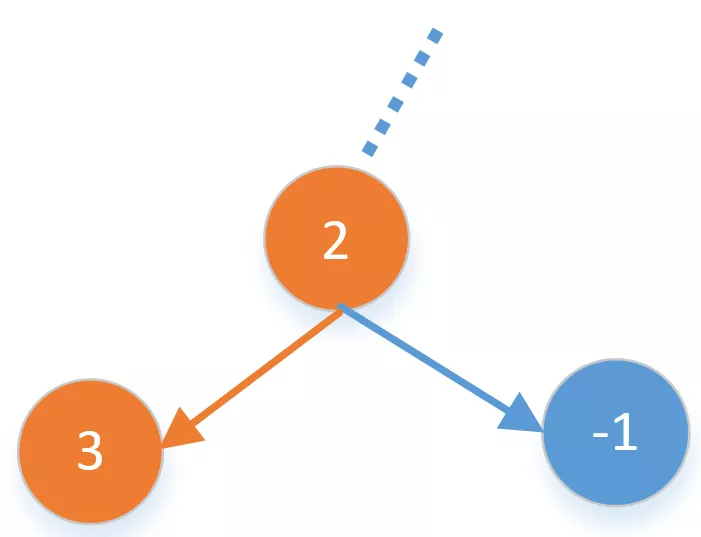
• 保留当前节点和右子节点。比如下面节点$2$的左子节点是负数，我们直接舍弃左子节点，但右子节点不是负数，我们可以保留右子节点。
  

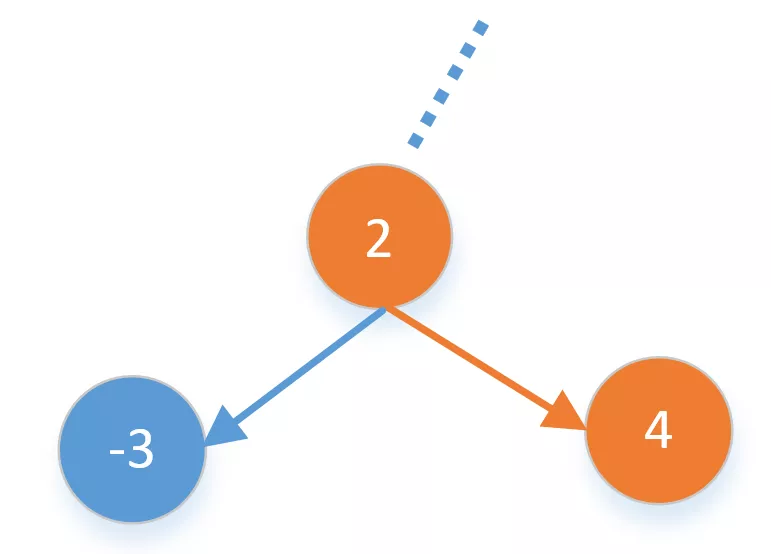
• 保留当前节点和两个子节点。比如下面节点$2$的左右子节点都不是负数，我们都可以留下。
  

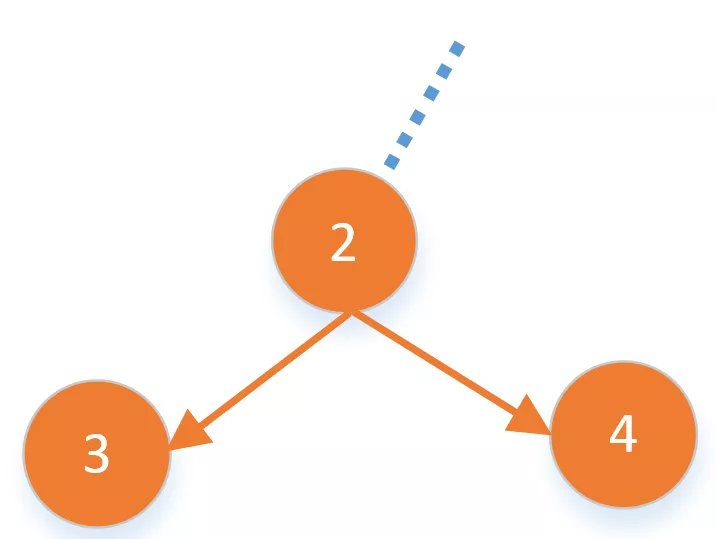
上面的$1, 2, 3$都可以作为子树的一部分再继续计算，我们可以使用同一个公式，取左右子节点最大的那个即可，如果都小于$0$我们就不要了，下面公式中$left$是左子树的值，$right$是右子树的值

int cur = root.val + Math.max(0, Math.max(left, right));

而$4$是不能再作为子树的一部分的参与计算的，因为已经分叉了，比如下面的$3 \to 2 \to 4$是不能再和节点$1$进行结合的。第$4$种情况如果左右子树有一个是小于$0$的我们不如不选，如果都大于$0$我们都要选。

int res = root.val + Math.max(0, left) + Math.max(0, right);

Java 代码

class Solution {
    private int maxValue = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        maxPathSumHelper(root);
        return maxValue;
    }

    public int maxPathSumHelper(TreeNode root) {
        if (root == null) return 0;
        // 左子节点的值
        int left = maxPathSumHelper(root.left);
        // 右子节点的值
        int right = maxPathSumHelper(root.right);
        // 第4种情况
        int cur = root.val + Math.max(0, left) + Math.max(0, right);
        // 第1，2，3三种情况，返回当前值加上左右子节点的最大值即可，如果左右子节点都小于0那就都不选
        int res = root.val + Math.max(0, Math.max(left, right));
        // 记录最大value值
        maxValue = Math.max(maxValue, Math.max(cur, res));
        // 第1, 2, 3种情况还可以再计算，所以返回的是res
        return res;
    }
}