题目描述
给定一个 n 个点的带权无向连通图,结点编号为 0 到 n-1,同时还有一个数组 edges,其中 edges[i] = [from_i, to_i, weight_i] 表示在 from_i 和 to_i 结点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集,它连接了所有结点且没有环,而且这些边的权值和最小。
请你找到给定图中最小生成树的所有关键边和伪关键边。如果最小生成树中删去某条边,会导致最小生成树的权值和增加,那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。
请注意,你可以分别以任意顺序返回关键边的下标和伪关键边的下标。
样例
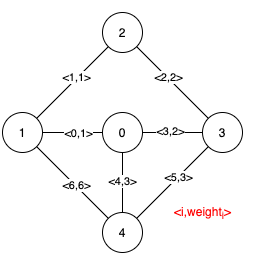
输入:n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
输出:[[0,1],[2,3,4,5]]
解释:上图描述了给定图。
下图是所有的最小生成树。
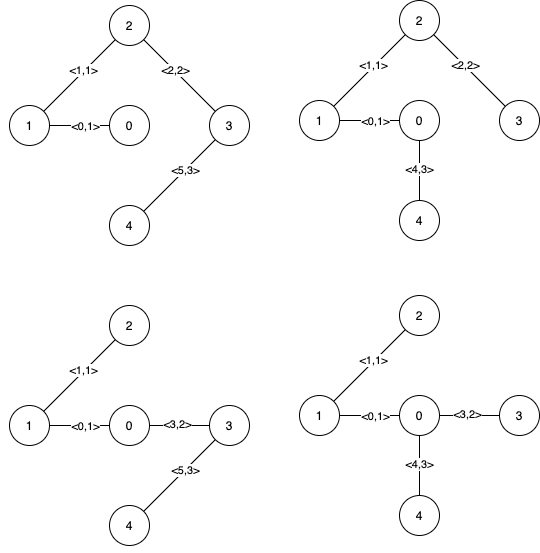
注意到第 0 条边和第 1 条边出现在了所有最小生成树中,所以它们是关键边。
我们将这两个下标作为输出的第一个列表。
边 2,3,4 和 5 是所有 MST 的剩余边,所以它们是伪关键边。
我们将它们作为输出的第二个列表。
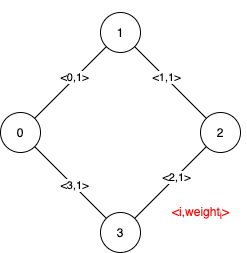
输入:n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
输出:[[],[0,1,2,3]]
解释:可以观察到 4 条边都有相同的权值,任选它们中的 3 条可以形成一棵 MST。所以 4 条边都是伪关键边。
限制
2 <= n <= 1001 <= edges.length <= min(200, n * (n - 1) / 2)edges[i].length == 30 <= from_i < to_i < n1 <= weight_i <= 1000- 所有
(from_i, to_i)数对都是互不相同的。
算法1
(最小生成树,图论,暴力枚举) $O(nm)$
- 先求出原图中任意一棵最小生成树
T,并记录下树边。 - 关建边集一定是
T的子集。 - 我们枚举每一条非树边
e(x, y, w),在T中通过深度优先搜索找到连接x和y的唯一一条路径。这条路径上的边权显然都是小于等于w的。如果路径上某条边e'的权重等于w,则e'只属于伪关建边,不再是关建边,同时e也属于伪关建边。
时间复杂度
- Prim 算法暴力求最小生成树的时间复杂度为 $O(n^2)$。
- 共有 $O(m)$ 条非树边,每条非树边都需要 $O(n)$ 的时间在树上寻找路径。
- 最终总时间复杂度为 $O(nm)$。
空间复杂度
- 需要 $O(n + m)$ 的额外空间。
C++ 代码
class Solution {
private:
void prim(vector<bool> &mst, int n,
const vector<vector<vector<int>>> &graph) {
vector<int> dis(n, INT_MAX), pre(n, -1);
vector<bool> vis(n, false);
dis[0] = 0;
for (int it = 0; it < n; it++) {
int ma = INT_MAX, u = -1;
for (int i = 0; i < n; i++)
if (!vis[i] && dis[i] < ma) {
ma = dis[i];
u = i;
}
vis[u] = true;
if (it > 0)
mst[pre[u]] = true;
for (const auto &e : graph[u]) {
int v = e[0], w = e[1], id = e[2];
if (dis[v] > w) {
dis[v] = w;
pre[v] = id;
}
}
}
}
bool dfs(int u, int target, const vector<bool> &mst,
const vector<vector<vector<int>>> &graph,
vector<int> &pre) {
if (u == target)
return true;
for (const auto &e : graph[u]) {
int v = e[0], w = e[1], id = e[2];
if (mst[id] && pre[v] == -1) {
pre[v] = id;
if (dfs(v, target, mst, graph, pre))
return true;
}
}
return false;
}
public:
vector<vector<int>> findCriticalAndPseudoCriticalEdges(
int n,
vector<vector<int>>& edges
) {
#define PSEUDO 1
#define CRITICAL 2
int m = edges.size();
vector<vector<vector<int>>> graph(n);
for (int i = 0; i < m; i++) {
int x = edges[i][0], y = edges[i][1], w = edges[i][2];
graph[x].push_back({y, w, i});
graph[y].push_back({x, w, i});
}
vector<bool> mst(m, false);
prim(mst, n, graph);
vector<int> res(m, 0);
for (int i = 0; i < m; i++)
if (mst[i])
res[i] = CRITICAL;
for (int i = 0; i < m; i++)
if (!mst[i]) {
int x = edges[i][0], y = edges[i][1], w = edges[i][2];
vector<int> pre(n, -1);
assert(dfs(x, y, mst, graph, pre) == true);
int u = y;
while (u != x) {
int nid = pre[u];
if (edges[nid][2] == w) {
res[nid] = PSEUDO;
res[i] = PSEUDO;
}
if (edges[nid][0] == u) u = edges[nid][1];
else u = edges[nid][0];
}
}
vector<vector<int>> ans(2);
for (int i = 0; i < m; i++)
if (res[i] == CRITICAL) ans[0].push_back(i);
else if (res[i] == PSEUDO) ans[1].push_back(i);
return ans;
}
};
算法2
(Kruskal 最小生成树,图论,桥) $O(m \log m)$
- 将所有边按照边权从小到大排序,按照边权分组。我们一次性考虑边权相同的一组边,对于同一组边我们考虑建一个新图。
- 对于边
(x, y),如果其两个端点x和y已经属于了同一个连通块,则这条边是冗余的(既不是关建边也不是伪关建边)。如果他们不属于同一个连通块,则在fx和fy之间建立一条边,fx和fy分别是这两个连通块的代表结点(并查集集合的根结点)。遍历完这一组边后,在建好的新图上求桥。桥边一定是关建边,非桥边就是伪关建边。 - 正确性也很显然,在最小生成树的正确性基础上,由于新图上的所有非冗余边的边权都是相同的,只要这些边的一部分能组成连通树,则其就一定是某棵最小生成树的一部分。我们直接将所有非冗余边都加入到了新图中,则边可以分为两类,一类是去掉后无论如何都无法再构成连通树,此类的边在新图中称为桥边,也就是关建边。剩余的一类边都是可以互相替代的,所以都是伪关建边。
时间复杂度
- 边权排序的时间复杂度为 $O(m \log m)$。
- 并查集查找的时间复杂度近似为常数。每次在新图上求桥的时间复杂度等于新图中点和边的数量。均摊来看,这部分总的时间复杂度为 $O(n + m)$。
- 故总时间复杂度为 $O(m \log m)$。
空间复杂度
- 需要 $O(n + m)$ 的额外空间。
C++ 代码
class Solution {
#define PSEUDO 1
#define CRITICAL 2
private:
vector<int> fa, sz;
vector<int> res;
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void tarjan(int u, int last_edge_id,
const unordered_map<int, vector<vector<int>>> &graph,
unordered_map<int, int> &dfn,
unordered_map<int, int> &low,
int &counter) {
dfn[u] = low[u] = ++counter;
for (const auto &e : (graph.find(u))->second) {
int v = e[0];
if (!dfn[v]) {
tarjan(v, e[1], graph, dfn, low, counter);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u])
res[e[1]] = CRITICAL;
} else if (last_edge_id != e[1]) {
low[u] = min(low[u], dfn[v]);
}
}
}
public:
vector<vector<int>> findCriticalAndPseudoCriticalEdges(
int n,
vector<vector<int>>& edges
) {
int m = edges.size();
vector<int> wid(m);
for (int i = 0; i < m; i++)
wid[i] = i;
sort(wid.begin(), wid.end(), [&](int x, int y) {
return edges[x][2] < edges[y][2];
});
fa.resize(n);
sz.resize(n, 1);
for (int i = 0; i < n; i++)
fa[i] = i;
res.resize(m, 0);
for (int i = 0, j = 0; i <= m; i++) {
if (i == m || edges[wid[i]][2] != edges[wid[j]][2]) {
unordered_map<int, vector<vector<int>>> graph;
unordered_map<int, int> dfn, low;
vector<int> v;
for (int k = j; k < i; k++) {
int fx = find(edges[wid[k]][0]), fy = find(edges[wid[k]][1]);
if (fx != fy) {
graph[fx].push_back({fy, wid[k]});
graph[fy].push_back({fx, wid[k]});
dfn[fx] = dfn[fy] = 0;
low[fx] = low[fy] = 0;
v.push_back(fx);
v.push_back(fy);
res[wid[k]] = PSEUDO;
}
}
int counter = 0;
for (int x : v)
if (!dfn[x])
tarjan(x, -1, graph, dfn, low, counter);
for (int k = j; k < i; k++) {
int fx = find(edges[wid[k]][0]), fy = find(edges[wid[k]][1]);
if (fx != fy) {
if (sz[fx] < sz[fy]) {
fa[fx] = fy;
sz[fy] += sz[fx];
} else {
fa[fy] = fx;
sz[fx] += sz[fy];
}
}
}
j = i;
}
}
vector<vector<int>> ans(2);
for (int i = 0; i < m; i++)
if (res[i] == CRITICAL) ans[0].push_back(i);
else if (res[i] == PSEUDO) ans[1].push_back(i);
return ans;
}
};

