题目描述

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：
如果你可以只使用 $O(n)$ 的额外空间（$n$ 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

算法

(动态规划，DP) $O(n^2)$

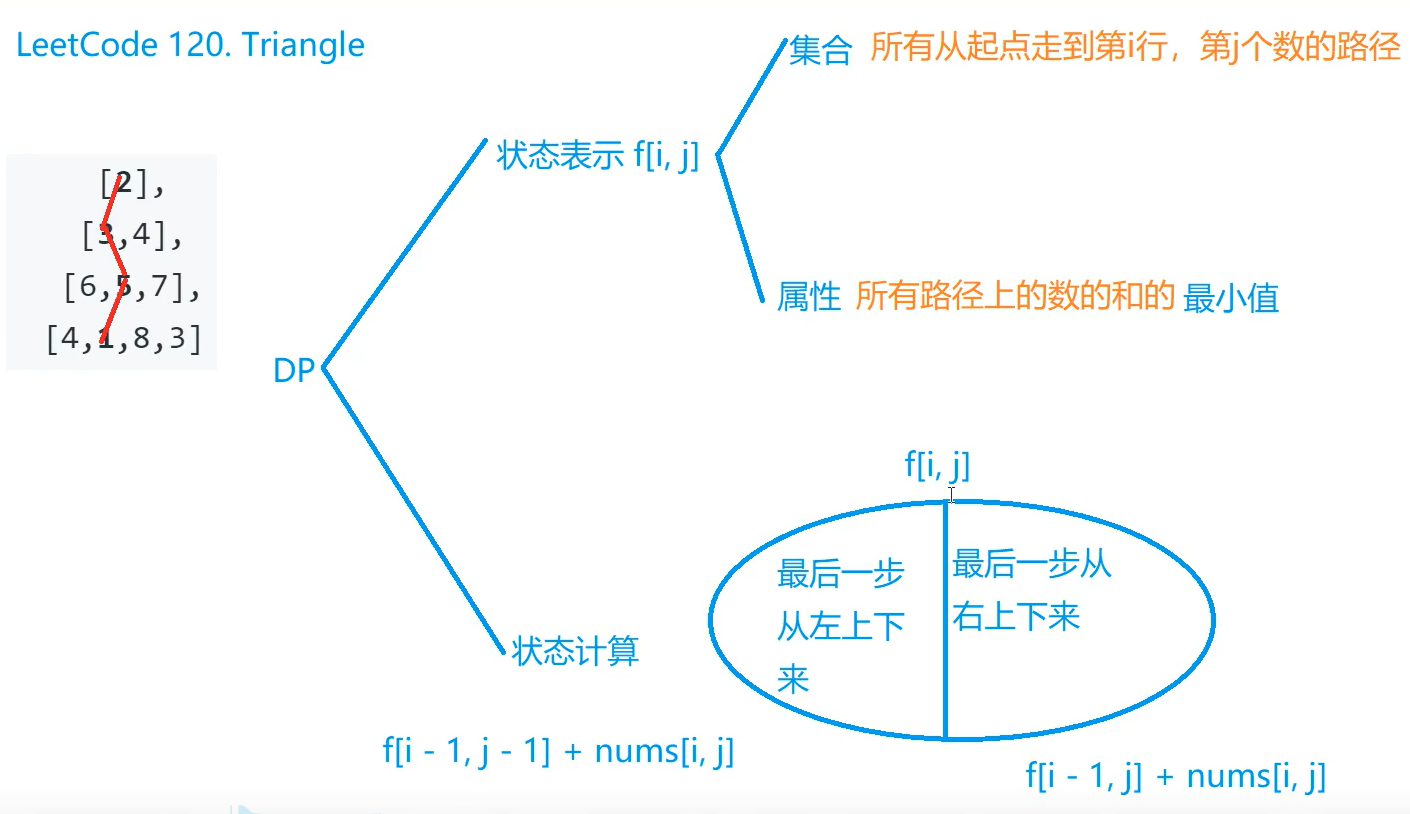
时间复杂度

时间复杂度$O(n^2)$，空间复杂度$O(n^2)$
由于第$i$层只用到了第$i-1$层，之前的层都没用到，被覆盖掉了，因此可以用两个滚动数组来优化，空间复杂度由$O(n^2)$降为$O(n)$

C++ 代码

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int n = triangle.size();
        vector<vector<long long>> f(n, vector<long long>(n));  // vector定义二维数组
        f[0][0] = triangle[0][0];  // 第0行只有一种方案
        for(int i = 1; i < n; i++)  // 从第一行开始做
            for(int j = 0; j <= i; j++)  // 遍历当前行前i个数
            {
                f[i][j] = INT_MAX;
                if(j > 0) f[i][j] = min(f[i][j], f[i - 1][j - 1] + triangle[i][j]);  // j>0才可以从左边更新(第一个数不能从左边过来)
                if(j < i) f[i][j] = min(f[i][j], f[i - 1][j] + triangle[i][j]);  // j<i才可以从右边更新(最后一个数不能从右边过来)
            }
        long long res = INT_MAX;  // 枚举最后一行的所有状态，取最小值
        for(int i = 0; i < n; i++) res = min(res, f[n - 1][i]);
        return res;
    }
};

优化后代码（只需要把所有第i层状态的下标&1即可）

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int n = triangle.size();
        vector<vector<long long>> f(2, vector<long long>(n));  // vector定义二维数组
        f[0][0] = triangle[0][0];  // 第0行只有一种方案
        for(int i = 1; i < n; i++)  // 从第一行开始做
            for(int j = 0; j <= i; j++)  // 遍历当前行前i个数
            {
                f[i & 1][j] = INT_MAX;
                if(j > 0) f[i & 1][j] = min(f[i & 1][j], f[i - 1 & 1][j - 1] + triangle[i][j]);  // j>0才可以从左边更新(第一个数不能从左边过来)
                if(j < i) f[i & 1][j] = min(f[i & 1][j], f[i - 1 & 1][j] + triangle[i][j]);  // j<i才可以从右边更新(最后一个数不能从右边过来)
            }
        long long res = INT_MAX;  // 枚举最后一行的所有状态，取最小值
        for(int i = 0; i < n; i++) res = min(res, f[n - 1 & 1][i]);
        return res;
    }
};