题目描述

某个局域网内有 n 台计算机和 k 条 双向 网线，计算机的编号是 1∼n。由于搭建局域网时工作人员的疏忽，现在局域网内的连接形成了回路，我们知道如果局域网形成回路那么数据将不停的在回路内传输，造成网络卡的现象。

注意：

对于某一个连接，虽然它是双向的，但我们不将其当做回路。本题中所描述的回路至少要包含两条不同的连接。
两台计算机之间最多只会存在一条连接。
不存在一条连接，它所连接的两端是同一台计算机。
因为连接计算机的网线本身不同，所以有一些连线不是很畅通，我们用 f(i,j) 表示 i,j 之间连接的畅通程度，f(i,j) 值越小表示 i,j 之间连接越通畅。

现在我们需要解决回路问题，我们将除去一些连线，使得网络中没有回路且不影响连通性（即如果之前某两个点是连通的，去完之后也必须是连通的），并且被除去网线的 Σf(i,j) 最大，请求出这个最大值。

输入格式
第一行两个正整数 n,k。

接下来的 k 行每行三个正整数 i,j,m 表示 i,j 两台计算机之间有网线联通，通畅程度为 m。

输出格式
一个正整数，表示被除去网线的 Σf(i,j) 的最大值。

数据范围
1≤n≤100
0≤k≤200
1≤f(i,j)≤1000
输入样例：
5 5
1 2 8
1 3 1
1 5 3
2 4 5
3 4 2
输出样例：
8

算法1

floyd算法，似乎只要跑一遍最小树，将最小树的权边计算出来，和总权值的差就是要去掉的边的权值

但是经过群友提示，这个图不是连通的，跑prim一遍得不到所有点的最小树。

我之前没看出来，局域网的电脑还带回路，还有不连通的局域网吗？？

那么稍微修改下prim
如果计算两点之间距离是无穷大 也就是不连通，那么不计算两点之间的权边，继续congtinue
本次prim完成后 找到那些st[0]为零 也就是标记还没在树的点 继续进行prim


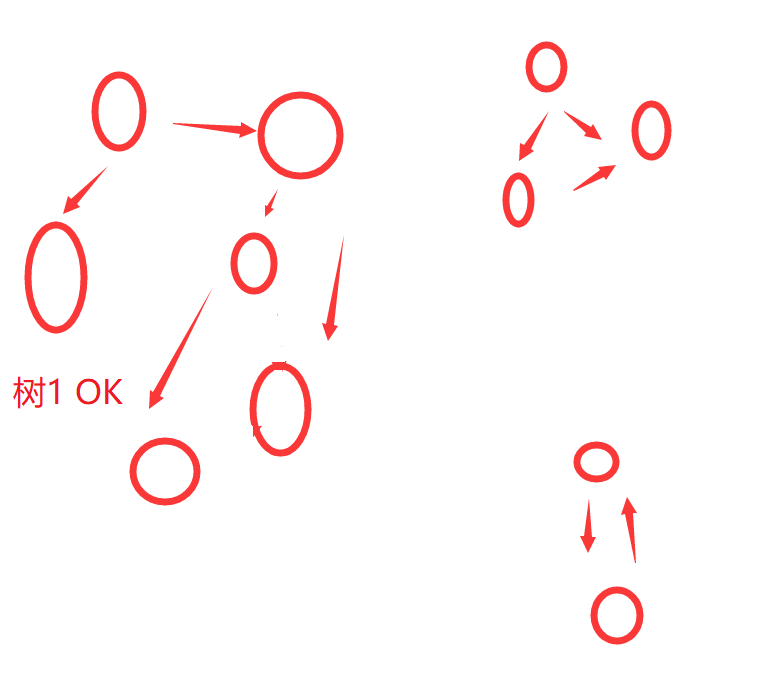
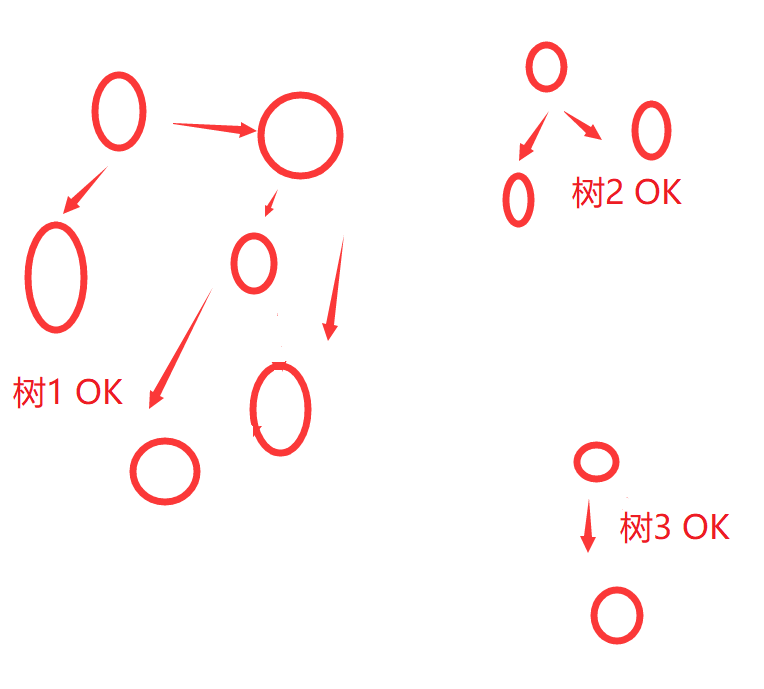
最后所有的点 都生成了最小树(可能不止一棵)
和total的差值就是答案

C++ 代码

// 112345.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
#include <vector>
#include <algorithm>
#include <memory.h>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;

int g[N][N];
int dist[N];
bool st[N];


int prim(int point)
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0;
    for (int i = 0; i < n; i++) {
        int t = -1;
        for (int j = 1; j <= n; j++) {
            if (!st[j] && (t == -1 || dist[t] > dist[j])) {
                t = j;
            }
        }

        if (i && dist[t] == INF) continue;
        if (i) res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; j++) dist[j] = min(dist[j],g[t][j]);
    }

    return res;
}

int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    int total;
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
        total += c;
    }

    for (int i = 1; i <= n; i++) {
        if (st[i] == 0)
            total -= prim(i);
    }

    cout << total << endl;


    return 0;
}