题目描述

一条包含字母 A-Z 的消息通过以下方式进行了编码：

'A' -> 1
'B' -> 2
...
'Z' -> 26

给定一个只包含数字的非空字符串，请计算解码方法的总数。

样例1

输入: "12"
输出: 2
解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。

样例2

输入: "226"
输出: 3
解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

算法

(动态规划) $O(n)$

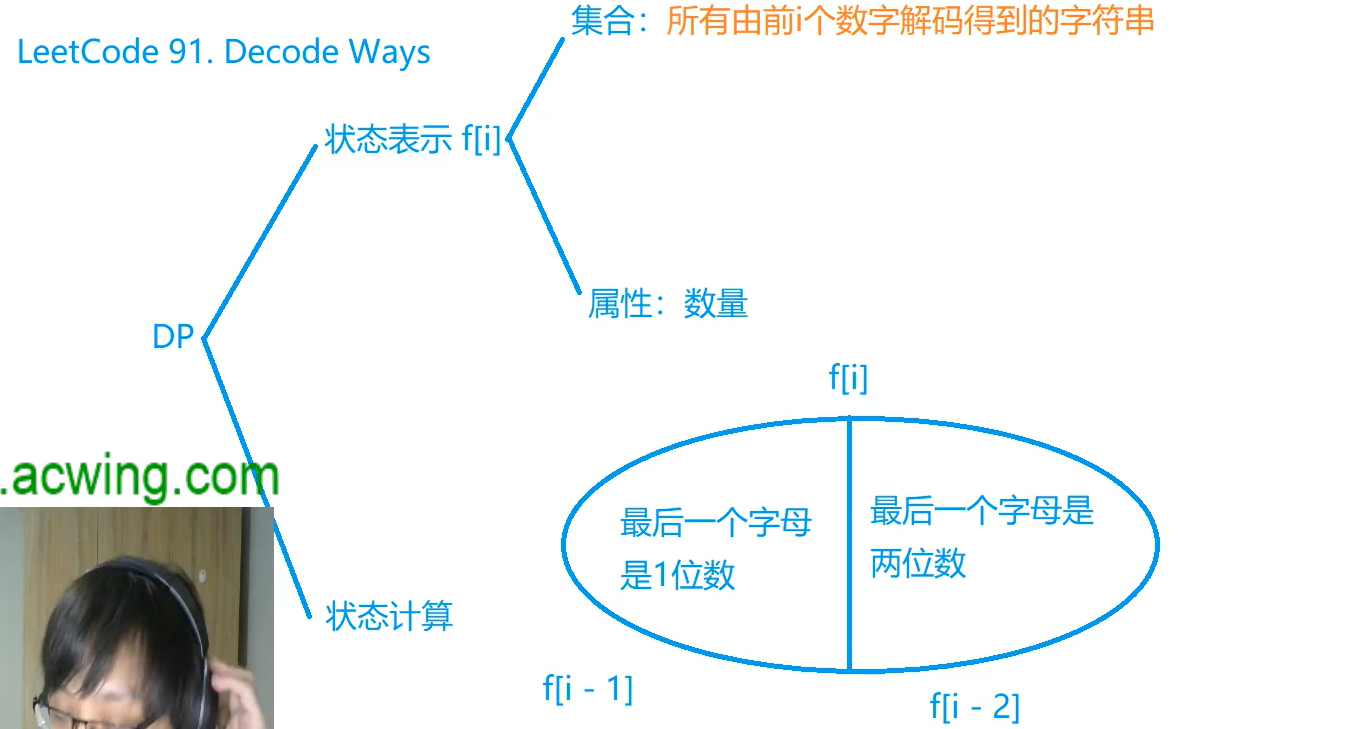
状态表示：$f[i]$ 表示前 $i$ 个数字共有多少种解码方式。
初始化：$0$个数字解码的方案数是$1$，即 $f[0]=1$。
状态转移：$f[i]$ 可以表示成如下两部分的和：

• 如果第 $i$ 个数字不是$0$，则 $i$ 个数字可以单独解码成一个字母，此时的方案数等于用前 $i−1$ 个数字解码的方案数，即 $f[i−1]$；
• 如果第 $i−1$ 个数字和第 $i$ 个数字组成的两位数在 $10$ 到 $26$ 之间，则可以将这两位数字解码成一个字符，此时的方案数等于用前 $i−2$ 个数字解码的方案数，即 $f[i−2]$；
  

时间复杂度

时间复杂度分析：状态数是 $n$ 个，状态转移的时间复杂度是 $O(1)$，所以总时间复杂度是$O(n)$。

C++ 代码

class Solution {
public:
    int numDecodings(string s) {
        int n = s.size();
        vector<int> f(n + 1);
        f[0] = 1;  // 没有数字对应空字符串
        for(int i = 1; i <= n; i++)
        {
            if(s[i-1] != '0') f[i] += f[i-1];  //第一种情况：最后一个字母是一位数
            if(i >= 2)  // 第二种情况：最后一个字母是两位数
            {
                int t = (s[i-2] - '0') * 10 + s[i-1] - '0';  // 算出最后一个字母的值
                if(t >= 10 && t <= 26) f[i] += f[i-2];  // 若是两位数，则是第二种情况的方案数
            }
        }
        return f[n];
    }
};