题目描述

给定一个无序的整数数组，找到其中最长上升子序列的长度。

样例

输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明:
可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 $O(n^2)$ 。
进阶: 你能将算法的时间复杂度降低到 $O(n log n)$ 吗?

算法

(动态规划) $O(n^2)$

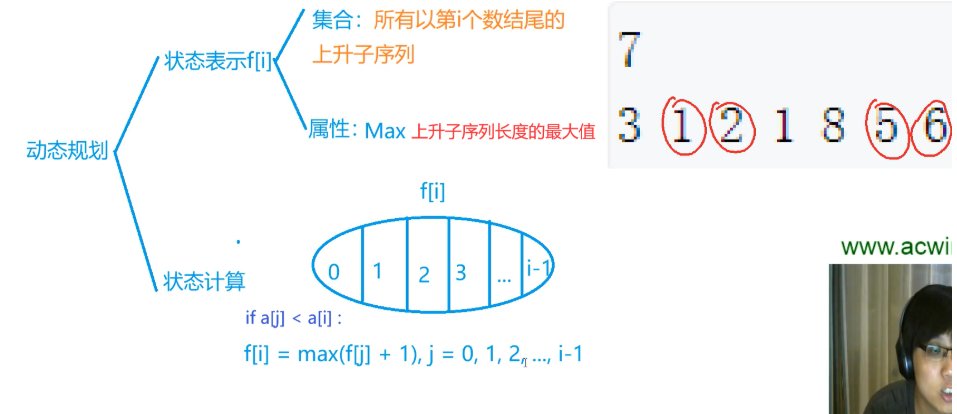
状态表示：$f[i]$表示所有以第i个数结尾的最长上升子序列长度的最大值。
状态计算：$f[i] =\max \{ f[j]+1 \}$

时间复杂度

时间复杂度为$O(n^2)$

参考文献

算法基础课：最长上升子序列

C++ 代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n);
        for(int i = 0; i < n; i++)
        {
            f[i] = 1;  // 只有a[i]一个数
            for(int j = 0; j < i; j++)
                if(nums[j] < nums[i])
                    f[i] = max(f[i], f[j] + 1);
        }
        int res = 0;
        for(int i = 0; i < n; i++) res = max(res, f[i]);  // 枚举所有的f[i]，取最大值
        return res;
    }
};