题目描述

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

样例

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

算法分析

找规律，如图所示

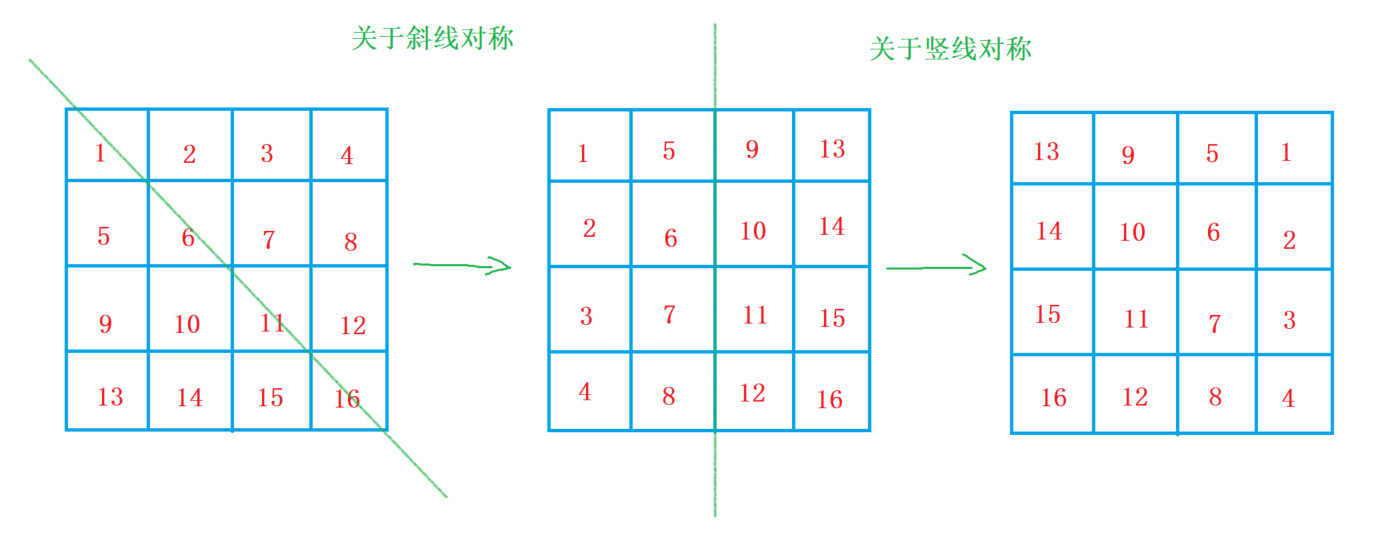
时间复杂度 $O(n^2)$

Java 代码

class Solution {
    static void swap(int[][] matrix,int x1,int y1,int x2,int y2)
    {
        int t = matrix[x1][y1];
        matrix[x1][y1] = matrix[x2][y2];
        matrix[x2][y2] = t;
    }
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        //斜对称
        for(int i = 0;i < n;i ++)
            for(int j = 0;j < i;j ++)
                swap(matrix,i,j,j,i);
        //竖对称
        for(int i = 0;i < n;i ++)
            for(int j = 0 ;j < n / 2;j ++)
                swap(matrix,i,j,i,n - 1 - j);

    }
}