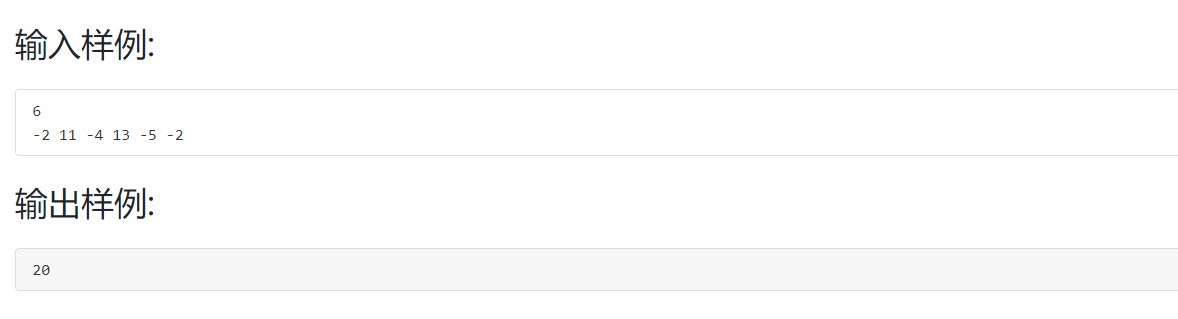
题目描述

样例

算法1

(在线处理) $O(n)$

时间复杂度$O(n)$

参考文献

C++ 代码

#include <iostream>

using namespace std;

const int N = 100010;

int q[N];

int main()
{
    int n;
    cin >> n;
    int x,MaxSum = 0, ThisSum = 0;
    for(int i=0;i<n;i++)
    {
        cin >> x;
        ThisSum += x;
        if(ThisSum > MaxSum) MaxSum = ThisSum;
        if(ThisSum < 0) ThisSum = 0;
    }

    cout<<MaxSum<<endl;

    return 0;
}

算法2

(分治法) $O(nlogn)$

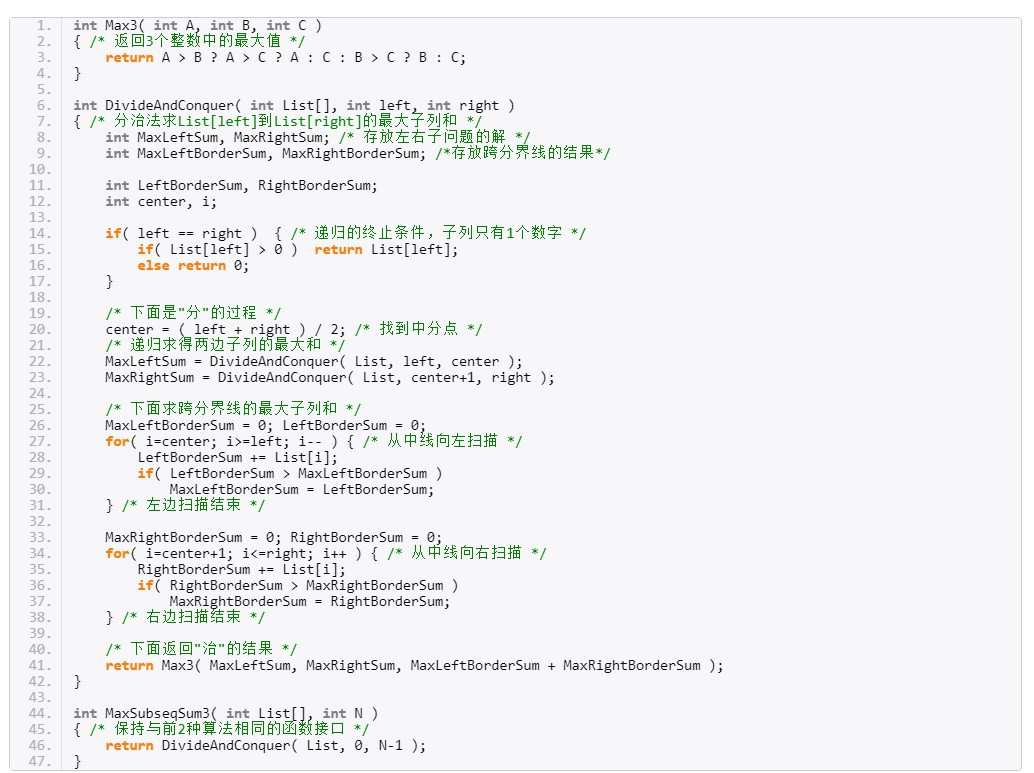
时间复杂度$O(nlogn)$

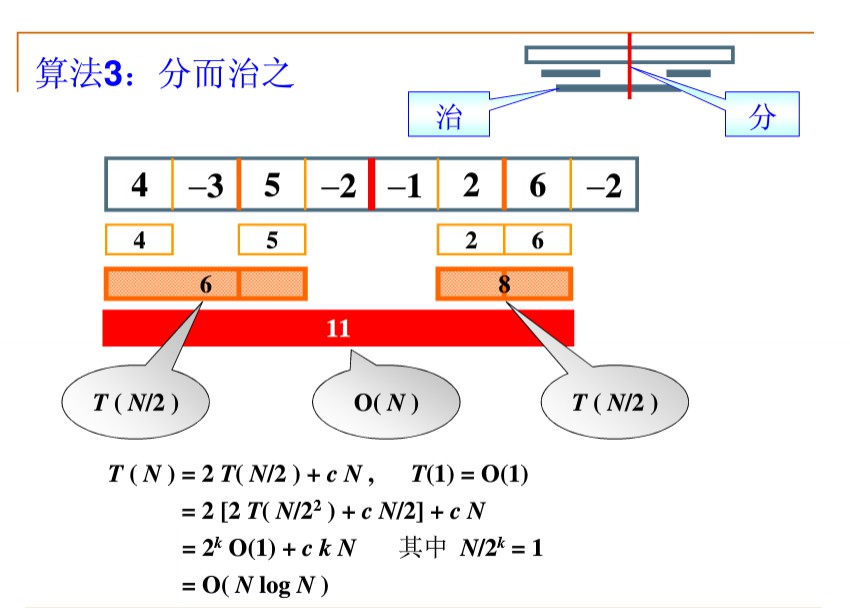
C++ 代码

#include <iostream>

using namespace std;

const int N = 100010;

int q[N];

int DivideAndConquer(int l,int r)
{
    if(l == r) // 递归终止条件，子列只有一个数字
    {
        if(q[l] > 0) return q[l];
        else return 0;
    }

    int mid = (l + r) / 2;
    // 递归求两边子列的最大和
    int left_sum = DivideAndConquer(l,mid);
    int right_sum = DivideAndConquer(mid + 1,r);

    // 求跨分界线的最大子列和
    int left_max_sum=0,right_max_sum=0;
    int left = 0,right = 0;
    for(int i=mid; i>= l; i--) // 从中线向左扫描
    {
        left += q[i];
        if(left > left_max_sum) left_max_sum = left;
    }

    for(int i=mid+1; i<= r; i++) // 从中线向右扫描
    {
        right += q[i];
        if(right > right_max_sum) right_max_sum = right;
    }

    // 返回"治”的结果
    return max(max(left_sum,right_sum), left_max_sum + right_max_sum);
}

int main()
{
    int n;
    cin >> n;
    for(int i=0;i<n;i++) cin >> q[i];

    cout<< DivideAndConquer(0,n-1);

    return 0;
}

课后练习 LeetCode 53.最大子序和