题目描述

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:

Input: coins = [1, 2, 5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1
Example 2:

Input: coins = [2], amount = 3
Output: -1
Note:
You may assume that you have an infinite number of each kind of coin.

算法1

(暴力枚举) TLE

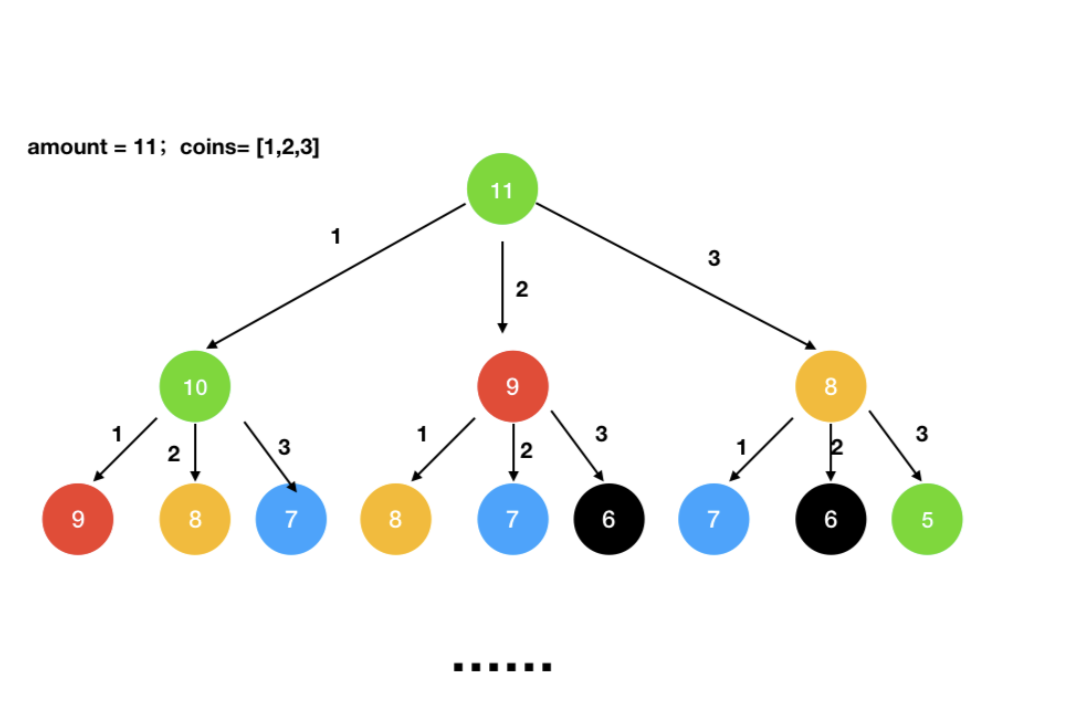
dfs搜索所有方案，会有大量的重复计算，比如节点7，8，9都被计算了好几次，所以会TLE

Java 代码

class Solution {

    private int res = 0x3f3f3f3f;

    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        if (n == 0) {
            return -1;
        }

        // 从coins中每个拿出若干个(cnt)拼凑出amount
        dfs(coins, amount, 0);

        return res == 0x3f3f3f3f ? -1 : res;
    }

    private void dfs(int[] coins, int amount, int cnt) {
        if (amount < 0) {
            // <0 不会影响res
            return;
        }

        if (amount == 0) {
            res = Math.min(res, cnt);
            return;
        }

        // 枚举每个面值的硬币
        for (int i = 0; i < coins.length; i++) {
            dfs(coins, amount - coins[i], cnt + 1);
        }
    }

}

算法2

动态规划

步骤1. 确定状态:
- 观察最后一步可以发现最后最少的那种方案答案，一定是用到coins中的某一个硬币(k)，所以问题可以转化成如何用coins中的面值的硬币凑出amount-coins[k], 所以问题规模变小了，变成了一个重复子问题:如何用coins中的面值的硬币凑出amount-coins[k]
那么显然可以归纳出状态dp[i]表示凑齐价值为i需要的最少硬币数目是多少？

步骤2. 确定状态转移方程:
- 因为最后一步可以发现最后最少的那种方案答案，一定是用到coins中的某一个硬币(k)的一个转移过来的，所以很容易想到，方程是: dp[i] = Math.min(dp[i - coins[0]], dp[i - coins[1]], dp[i - coins[2]], ......) + 1。

步骤3. 考虑边界和初始状态:
- (i - coins[j])如果是负数怎么办？
- 没法评出题目要求的amount怎么办，比如dp[amount]完全拼不出？
- 初始值dp[0] = 0。
要解决上面的问题，我们必须人为规定dp[负数], dp[凑不出的amount]为一个很大的值，比如0x3f3f3f3f。

步骤4. 考虑计算顺序:
- 这方案属于bottom-up解法，所以是从小到大枚举，dp[0]计算到dp[amount],我们计算dp[i]的时候dp[i - coins[0]], dp[i - coins[1]], dp[i - coins[2]]…都已计算出来了，就算没计算
也规定初始值是0x3f3f3f3了。

例子1：假设 coins = [1, 2, 5], amount = 11

F(i) 最小硬币数量
F(负数) 0x3f3f3f3f
F(0) 0 //金额为0不能由硬币组成
F(1) 1 //F(1)=min(F(1-1),F(1-2),F(1-5))+1=1F(1)=min(F(1−1),F(1−2),F(1−5))+1=1
F(2) 1 //F(2)=min(F(2-1),F(2-2),F(2-5))+1=1F(2)=min(F(2−1),F(2−2),F(2−5))+1=1
F(3) 2 //F(3)=min(F(3-1),F(3-2),F(3-5))+1=2F(3)=min(F(3−1),F(3−2),F(3−5))+1=2
F(4) 2 //F(4)=min(F(4-1),F(4-2),F(4-5))+1=2F(4)=min(F(4−1),F(4−2),F(4−5))+1=2
… …
F(11) 3 //F(11)=min(F(11-1),F(11-2),F(11-5))+1=3F(11)=min(F(11−1),F(11−2),F(11−5))+1=3

时间复杂度O(coins.length() * coins)

java 代码

public class Solution {

    int[] dp = null;

    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        if (n == 0) {
            return -1;
        }

        // 凑齐总价值 i 需要的最少硬币数
        dp = new int[amount + 1];
        dp[0] = 0;

        // 从小到大枚举每个amount中的价值
        for (int i = 1; i < amount; i++) {
            dp[i] = 0x3f3f3f3f;

            // 尝试每个硬币
            for (int j = 0; j < n; j++) {
                if (i >= coins[j] && dp[i - coins[j]] < 0x3f3f3f3f) {
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }

        if (dp[amount] >= 0x3f3f3f3f) {
            return -1;
        } else {
            return dp[amount];
        }
    }

}