题目描述

你总共需要上 n 门课，课程编号依次为 0 到 n-1 。

有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以 [1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。

对于每个查询对 queries[i]，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。

样例1

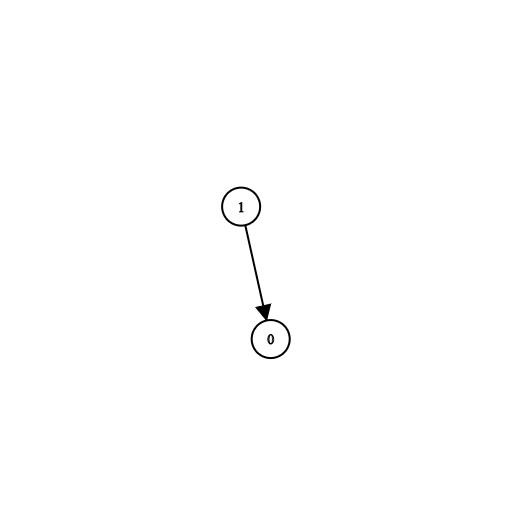
输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

样例2

输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

样例3

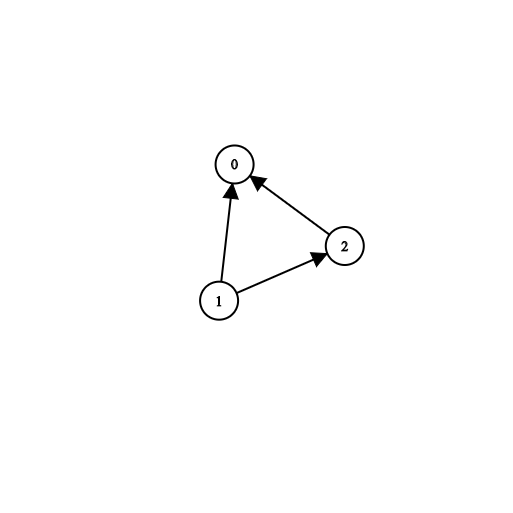
输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

样例4

输入：n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出：[false,true]

样例5

输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]

限制

• 2 <= n <= 100
• 0 <= prerequisite.length <= (n * (n - 1) / 2)
• 0 <= prerequisite[i][0], prerequisite[i][1] < n
• prerequisite[i][0] != prerequisite[i][1]
• 先修课程图中没有环。
• 先修课程图中没有重复的边。
• 1 <= queries.length <= 10^4
• queries[i][0] != queries[i][1]

算法1

bfs $O(n · (n + m))$

1. 使用邻接表存储图
2. 对每个点都进行一次 bfs：对 i 遍历所有邻边，让所有邻边的邻边a都打表 st[i][a] = true

时间复杂度

• 建图，需要遍历所有边 prerequisites 时间复杂度是 $O(m)$
• 查询，需要遍历所有询问 queries, 时间复杂度是 $O(10^4)$, 记为 $O(q)$
• 对每个点的打表预处理：
  • 每个顶点都会入队1次，时间复杂度是 $O(n)$
  • 对该顶点进行一次 bfs，每条边仅会入队一次出队一次, 时间复杂度是 $O(m + n)$
  • 故时间复杂度是 $O(n · (n + m))$
• 故总的时间复杂度是 $O(n · (n + m) + m + q)$

空间复杂度

• 需要用邻接表存储图，空间复杂度为 $O(n · m)$
• 需要用二维数组预处理打表，空间复杂度为 $O(n²)$
• 需要记录答案，空间复杂度为 $O(q)$
• 故需要额外的空间复杂度是 $O(n² + (n · m) + q)$

其他

• 邻接表，可参考AcWing 826. 单链表
• 广度优先遍历 bfs，可参考AcWing 847. 图中点的层次

C++ 代码

class Solution {
public:
    const static int N = 110, M = 1e4 + 10;
    int h[N], e[M], ne[M], idx;  // 邻接表(数组模拟链表)
    bool st[N][N];

    void add(int a, int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    void bfs(int n)
    {
        queue<int> q;
        for (int i = 0; i < n; i ++)
        {
            q.push(i);

            while(q.size())
            {
                int t = q.front();
                q.pop();

                for (int head = h[t]; head != -1; head = ne[head])
                {
                    int j = e[head];
                    if (!st[i][j])
                    {
                        st[i][j] = true;
                        q.push(j);
                    }
                }
            }
        }
    }

    vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {

        vector<bool> res;
        memset(h, -1, sizeof(h));

        for (int i = 0; i < prerequisites.size(); i ++)
        {
            int a = prerequisites[i][0], b = prerequisites[i][1];
            add(a, b);
        }

        bfs(n);

        for (int i = 0; i < queries.size(); i ++)
        {
            int head = queries[i][0];
            int target = queries[i][1];
            res.push_back(st[head][target]);
        }

        return res;
    }
};

算法2

Floyd(传递背包) $O(n³)$

1. 目的是找出当前课程所有的依赖课程，即给出课程a b c的依赖关系a->b，b->c 就要能判断a->c；
2. 这是一个多起点的图论问题，再看看数据范围n<=100，因此很自然会想到Floyd，判断某个点a能不能到达点b；
3. 处理图的存储：使用邻接矩阵来存储所有课程的关系，d[a][b]：表示上b课程是否需要先上a课程；
4. Floyd的过程其实很简单，三层循环，然后判断如果i->k && k->j 那么 i->j 。

时间复杂度

• 建图，需要遍历所有边 prerequisites 时间复杂度是 $O(m)$
• Floyd 过程的时间复杂度是 $O(n³)$
• 查询，需要遍历所有询问 queries , 时间复杂度是 $O(10^4)$, 记为 $O(q)$
• 故需要的时间复杂度是 $O(n³ + m + q))$

空间复杂度

• 需要用邻接矩阵存所有边的关系，空间复杂度为 $O(n²)$
• 存储答案需要空间复杂度为 $O(n)$
• 故需要额外的空间复杂度是 $O(n² + n))$

其他

• Floyd 的模板题, 可以参考AcWing 854. Floyd求最短路
• 传递背包，可以参考AcWing 343. 排序

Go 代码

func checkIfPrerequisite(n int, ps [][]int, qs [][]int) []bool {
    d := make([][]bool, n)
    for i := 0; i < n; i ++ {
        d[i] = make([]bool, n)
    }

    for i, _ := range ps {
        a := ps[i][0]
        b := ps[i][1]
        d[a][b] = true
    }

    for k := 0; k < n; k ++ {
        for i := 0; i < n; i ++ {
            for j := 0; j < n; j ++ {
                if d[i][k] && d[k][j] {
                    d[i][j] = true
                }
            }
        }
    }

    res := []bool{}
    for i, _ := range qs {
        a := qs[i][0]
        b := qs[i][1]
        res = append(res, d[a][b])
    }

    return res
}