题目描述

给出 n 个互不相同的正整数。

问存在多少个子集，使得子集中所有数的异或和是质数。

由于答案可能很大，请你输出对 1e9 + 7 取模后的结果

样例

输入：
3
1 2 3
输出：
4

解释：
共有6个子集: 
[1]:1, [2]:2, [3]:3, [1,2]:3, [1,3]:2, [2,3]:1, [1,2,3]:0
其中, 2, 3是质数，所以有4个子集
分别是：[2]、[3]、[1,2]、[1,3]

限制

• 1 ≤ n ≤ 5000
• 1 ≤ 给定正整数 ≤ 5000

算法

(01背包+试除法判定质数)

1. 数据范围最大的数是5000, 而2^12 = 4096，因此考虑异或和最大的数是 2^13 - 1（因为异或是不进位加法，所以无论怎么异或都不可能超过最大的数表示二进制位全是1的数）
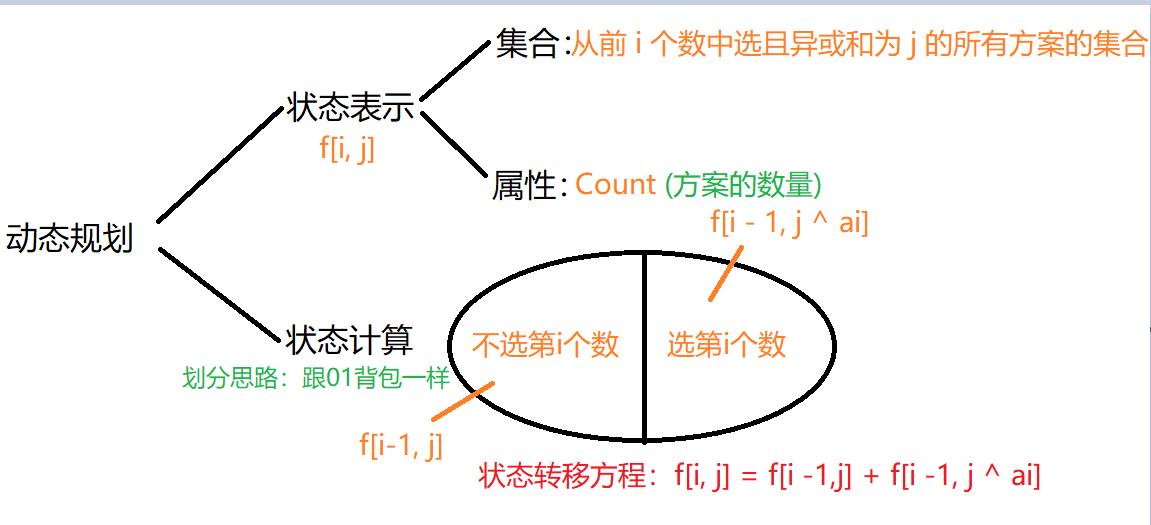
2. 所有组成的子集里找出异或和包含在[0, 2^13-1]有多少个。对应01背包，从n个物品中选k个物品符合某些限制的方案数，上图给出闫式dp分析法

其他

• 异或和就是所有数异或起来；
• go 的 & 运算符优先级比 + - 高；
• 01背包问题：可以参考AcWing 2. 01背包问题
• 试除法判定质数：可以参考AcWing 866. 试除法判定质数

时间复杂度

• 二维状态的第二维空间至少是 $2^{13}$， 记为 m
• dp过程的时间复杂度：
  • 状态数是 $O(n · m)$
  • 状态计算是 $O(1)$
• 试除法的时间复杂度是 $O(m · sqrt(m))$
• 故总的时间复杂度为: $O(n · m) + O(m · sqrt(m))$

空间复杂度

• 二维状态的第二维空间至少是 $2^{13}$， 记为 m
• 存储长度为 n 的正整数集合，需要 $O(n)$
• 状态表示需要开二维数组, $O(2 · m)$
  • 2是因为要使用滚动数组优化, 不用滚动数组就会 MLE ： 5000 x 8192 ≈ 156MB > 64MB
  • 滚动数组并不会改变时间复杂度，但可以优化空间复杂度
• 故总的空间复杂度为 $O(2m + n)$

Go 代码

package main

import "fmt"

const (
    N int = 5010
    M int = 8200
    MOD int = 1e9 + 7
)

var (
    n int
    f [2][M]int
    a [N]int
)

func is_prime(x int) bool {
    for i := 2; i <= x / i; i ++ {
        if x % i == 0 {
            return false
        }
    }

    return true
}

func main() {
    fmt.Scanf("%d", &n)

    for i := 1; i <= n; i ++ {
        fmt.Scanf("%d", &a[i])
    }

    f[0][0] = 1    
    for i := 1; i <= n; i ++ {
        for j := 0; j < M; j ++ {
            f[i & 1][j] = f[(i - 1) & 1][j]
            if j ^ a[i] < M {
                f[i & 1][j] = (f[(i - 1) & 1][j] + f[(i - 1) & 1][j ^ a[i]]) % MOD
            }
        }
    }

    res := 0
    for i := 2; i < M; i ++ {
        if is_prime(i) {
            res = (res + f[n & 1][i]) % MOD
        }
    }

    fmt.Printf("%d", res)
}