题目描述

给你一个整数 n 表示某所大学里课程的数目，编号为 1 到 n，数组 dependencies 中，dependencies[i] = [x_i, y_i] 表示一个先修课的关系，也就是课程 x_i 必须在课程 y_i 之前上。同时你还有一个整数 k。

在一个学期中，你 最多 可以同时上 k 门课，前提是这些课的先修课在之前的学期里已经上过了。

返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。

样例

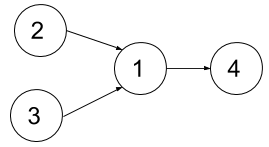
输入：n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2
输出：3 
解释：上图展示了题目输入的图。
在第一个学期中，我们可以上课程 2 和课程 3。
然后第二个学期上课程 1 ，第三个学期上课程 4。

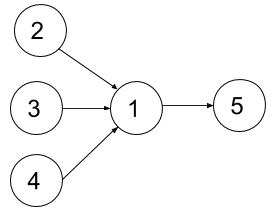
输入：n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2
输出：4 
解释：上图展示了题目输入的图。
一个最优方案是：第一学期上课程 2 和 3，第二学期上课程 4，第三学期上课程 1，第四学期上课程 5。

输入：n = 11, dependencies = [], k = 2
输出：6

限制

• 1 <= n <= 15
• 1 <= k <= n
• 0 <= dependencies.length <= n * (n-1) / 2
• dependencies[i].length == 2
• 1 <= x_i, y_i <= n
• x_i != y_i
• 所有先修关系都是不同的，也就是说 dependencies[i] != dependencies[j]。
• 题目输入的图是个有向无环图。

算法

(状态压缩动态规划) $O(n \cdot 2^n + 3^n)$

1. 统计出每个课程的直接依赖课程的二进制掩码，记为 pre。
2. 设状态 $f(S)$ 表示完成掩码 $S$ 的课程所需要的最少学期数。
3. 初始时，$f(0) = 0$，其余为正无穷。
4. 转移时，对于某个已经修完的课程掩码 $S_0$，求出 $S_1$，表示当前可以选择的新课程（新课程需要满足依赖条件），从 $S_1$ 中通过递归回溯选出不多于 $k$ 门课程，其掩码记为 $S$，转移 $f(S_0 \text{ bit or } S) = \min(f(S_0 \text{ bit or } S), f(S_0) + 1)$。
5. 最终答案为 $f((1 << n) - 1)$。

时间复杂度

• 状态数有 $O(2^n)$ 个，采用向后转移的方式，每个状态需要 $O(n)$ 的时间计算 $S_1$，同时枚举 $S_1$ 的合法子集。
• 容易证明子集共有 $O(3^n)$ 个。
• 故总时间复杂度为 $O(n \cdot 2^n + 3^n)$，由于合法子集数目非常少，采用递归回溯枚举子集不会出现不合法的子集，则复杂度的常数很小。

空间复杂度

• 需要 $O(2^n)$ 的额外空间存储 pre 数组，系统栈和动态规划的状态。

C++ 代码

class Solution {
private:
    void solve(int i, int s, int k, int n, int s0, int s1, vector<int> &f) {
        if (k == 0 || i == n) {
            f[s0 | s] = min(f[s0 | s], f[s0] + 1);
            return;
        }

        solve(i + 1, s, k, n, s0, s1, f);

        if ((s1 >> i) & 1)
            solve(i + 1, s | 1 << i, k - 1, n, s0, s1, f);
    }

public:
    int minNumberOfSemesters(int n, vector<vector<int>>& dependencies, int k) {
        vector<int> pre(n, 0);

        for (const auto &v : dependencies)
            pre[v[1] - 1] |= 1 << (v[0] - 1);

        vector<int> f(1 << n, INT_MAX);

        f[0] = 0;
        for (int s0 = 0; s0 < (1 << n); s0++) {
            if (f[s0] == INT_MAX)
                continue;

            int s1 = 0;
            for (int i = 0; i < n; i++)
                if (!((s0 >> i) & 1) && ((pre[i] & s0) == pre[i]))
                    s1 |= 1 << i;

            solve(0, 0, k, n, s0, s1, f);
        }

        return f[(1 << n) - 1];
    }
};