题目描述

小招正在玩一款修塔游戏，系统中有 n 座高塔，每座高塔由若干个高度相同的方块堆砌而成，修塔游戏的规则为：

每次从最高塔的塔尖拿走一个方块
每次在最低塔的塔尖堆砌一个方块
小招每次只能完成上述两个动作中的一个动作。

游戏的目标是使 n 座高塔中至少有 k 座高塔的高度相同，请问小招最少需要多少次才能完成游戏。

输入格式
输入共有 2 行，第一行为 n 和 k，第二行为 n 座塔的高度组成的数组 a1,a2,…an。

输出格式
输出值为最少需要多少次动作才能完成游戏。

数据范围
1≤k≤n≤200000,
1≤aj≤10000

样例

输入样例：
6 5
1 2 2 4 2 3
输出样例：
3

算法1

$O(n)$

要求最小操作次数，先假设最终结果k个塔一样高时，这k个塔的高度是h。我们可以分三个部分来考虑：
然后在这三部分里面求一个最小值就行了，为了方便考虑，我们先把塔排序，设i是中间分界点

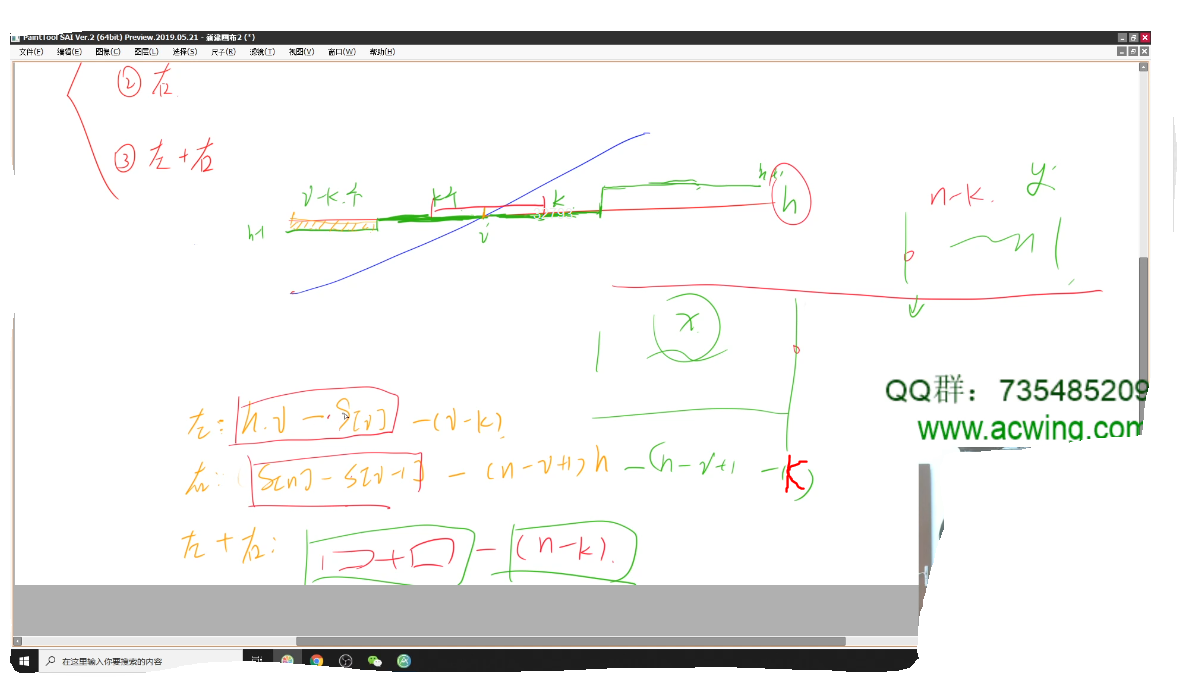
1.考虑左边，这k个塔都在左边，即我们通过堆砌来达到h高度，因为我们每次只能在最低塔的塔尖堆砌一个方块，所以左边的塔只能一层一层的堆砌，当k个塔达到h高度时，左边的i-k个塔的高度一定是h-1（这个很关键，只有想出这个问题才能做出来）那我们怎么算出操作多少次呢？因为每次只能把塔高度增加1或减1，我们可以把操作次数传化为求增加了多少高度，然而增加了多少高度不太好计算，我们反过来想，先求出整个高度和（前面i个塔 * h高度）减去前面i个塔的高度 在减去还没有增加的塔高度和（即前面提高的（i-k）* 1）。前面i个塔的高度我们可以用前缀和来表示。最后公式就是：
左边：h * i - s[i] - (i - k)

2.考虑右边，推理同上，右边整个高度和：s[n] - s[i- 1]，有 n - i + 1 - k 个塔不需要拿走一个方块，所以
右边：s[n] - s[i- 1] - (n - i + 1) * h -（n - i + 1 - k）

3.左边一部分，右边一部分。因为不管左边取多少塔或者右边取多少塔，结果都是一样的：
左边+ 右边： h * i - s[i] + s[n] - s[i- 1] - （n - k)

最后我们可以通过枚举所有塔的高度，题目塔的范围是1到10000，来求一个最优解，最后我们求所有塔的高度时，不需要先排序，用桶排序的思想
统计每一个塔有多少个，来计算高度和，这样时间复杂减少到o(n)。

时间复杂度

Java 代码

import java.util.*;

public class Main{
    static int N = 10010;
    public static void main(String[] args){
        Scanner sin = new Scanner(System.in);
        int n = sin.nextInt();
        int k = sin.nextInt();
        int[] c = new int[N];
        int[] s = new int[N];
        int maxCnt = 0; //同一高度的塔最大的数量
        for(int i = 0; i < n; ++ i){
            int h = sin.nextInt();
            //同一高度塔的数量
            c[h] ++;
            maxCnt = Math.max(maxCnt, c[h]);
        }
        //已经有大于k个塔的高度相等了，不需要操作
        if (maxCnt >= k) {
            System.out.println(0);
            return;
        }

        //计算前缀和：前h高度的塔的所有高度和，h代表塔的高度，c[h]表示h高度的塔的数量
        for(int h = 1; h <= 10000; ++h){
            s[h] = s[h - 1] + h * c[h];
        }
        //从题目给出的范围，最大的操作次数是20亿次，即抹平，要求最小次数，我们先把结果设置最大
        int res = (int)2e9;
        //枚举所有塔的高度，其中h代表塔的高度，cnt代表小于当前高度h的塔的数量是多少
        for(int h = 1, cnt = 0; h <= 10000; ++ h){
            int left = cnt * h - s[h - 1];
            int right = s[10000] - s[h] - (n - cnt - c[h]) * h;
            //如果左边满足条件
            if(cnt + c[h] >= k) {
                res = Math.min(res, left - (cnt + c[h] - k));
            }
            //右边满足条件
            if (n - cnt >= k) {
                res = Math.min(res, right - (n - cnt - k));
            }
            //左右两边
            res = Math.min(res, left + right - (n - k));
            //更新cnt
            cnt += c[h];
        }
        System.out.println(res);
    }
}