题目描述 如题
递归树以及剪枝如图示:
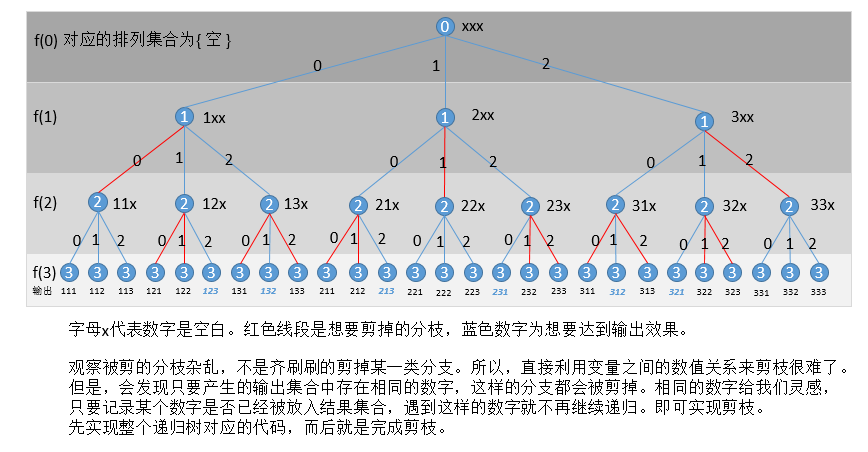
考虑递归函数的实现:
首先,观察样例输出。发现都是长度为3的一串数组。结合递归树,发现是在递归到f(3)才输出。之前的状态
都没有输出。体会到该处存在一个限制:递归参数u等于集合元素的总个数n的时候才能输出数字串。
该函数必然有输出模块,同时还有递归模块。输出模块是递归函数的出口。
递归模块可以通过在区间[0, n)上迭代递归函数本身。
于是,代码就长成了如下的样子:
先写出不剪枝的递归树对应的代码
C++ 代码
const int N = 10;
int a[N]; // 保存结果的集合
int n;
void dfs(int u) {
if(u == n) {
for(int i = 0; i < n; i++)
cout << a[i] << " ";
puts("");
return;
}
for(int i = 0; i < n; i++) {
a[u] = i + 1;
dfs(u + 1);
}
}
输入样例:
3
输出样例:
n = 3的时候,输入就是递归树输出行的所有集合,3 ^ 3 = 27 个数字串。
对上面的代码剪枝
C++ 代码
const int N = 10;
int a[N], s[N], n;
void dfs(int u) {
if(u == n) {
for(int i = 0; i < n; i++)
cout << a[i] << " ";
puts("");
return;
}
for(int i = 0; i < n; i++) {
if(s[i]) continue;
s[i] = 1;
a[u] = i + 1;
dfs(u + 1);
s[i] = 0;
}
}
输入样例:
3
输出样例:
n = 3时,输出递归树中所有蓝色的数字串。
总结:
样例给出的输出并不代表某种一般性的问题。可能得先解决一个更一般的问题。当然,这里可以体会到理解模板
熟记模板的重要性。熟记模板的前提是充分理解模板的实质!然后才是背板子,加快解决问题的速度。
搞清楚来龙去脉,最后才有复制粘贴板子的底气。
该问题的推广极简模板
void dfs(int u) {
if(u == n) return;
for(int i = 0; i < n; i++)
dfs(u + 1);
}


感谢大佬的分享,整明白了