最小生成树

下面两种算法只能处理无向图，处理有向图的话可以用朱刘算法
prim算法
每次找到距离集合最小的点，把它加入到集合中并更新其他点。
为什么是正确的？

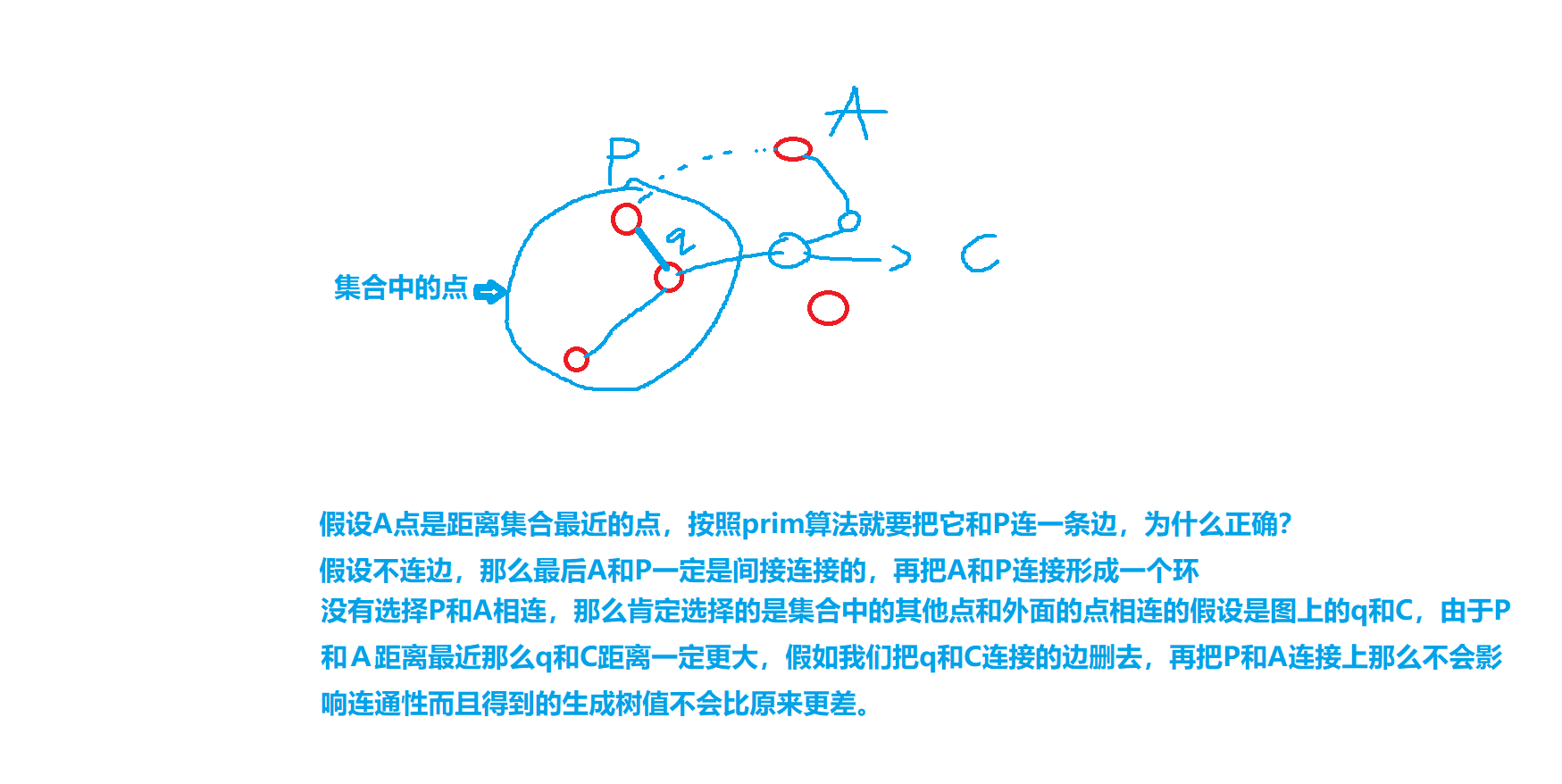
kruskal算法
把所有边从小到大排序
依次枚举每条边，如果这条边的两个点不在同一个集合中，就把他们加到同一个集合（并查集维护）
正确性？

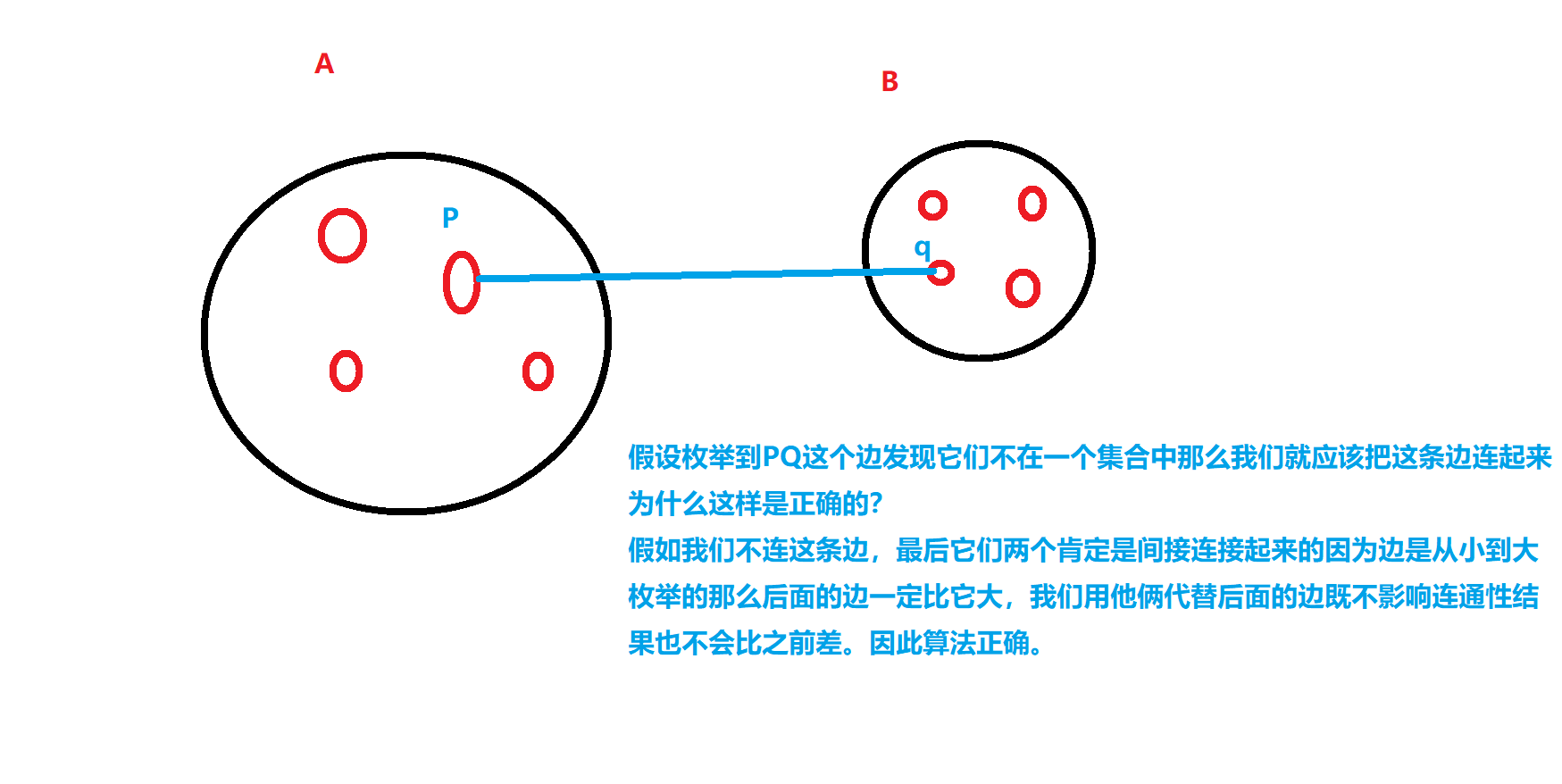
kruskal这个算法比较灵活能扩展很多处。
1）求一个无向连通图的最小生成树或者求一个无向非联通图的最小生成森林都可以。
2）求一个无向图的生成树要求生成树的边权最大值最小。直接用最小生成树算法做即可。
为什么是对的？
理由：枚举到这个边，发现他的两个点不在一个集合中，我们就应该把这条边加入，因为后面的边权都比它大，所以这个一定是最优的。
3）这个算法具有局部最优性质，即使前面已经维护好了一个集合，再用kruskal算法也是对的。可以用上述方法证明。
注意：如果一个无向图的边权可正可负，求在保证连通性的情况下，权值最小，这不可以用最小生成树求解。
因为假如边权全部为负的话，那么把所有边权假如值一定最小。