题目描述

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

Insert a character
Delete a character
Replace a character

样例

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

算法

(动态规划) O(mn)

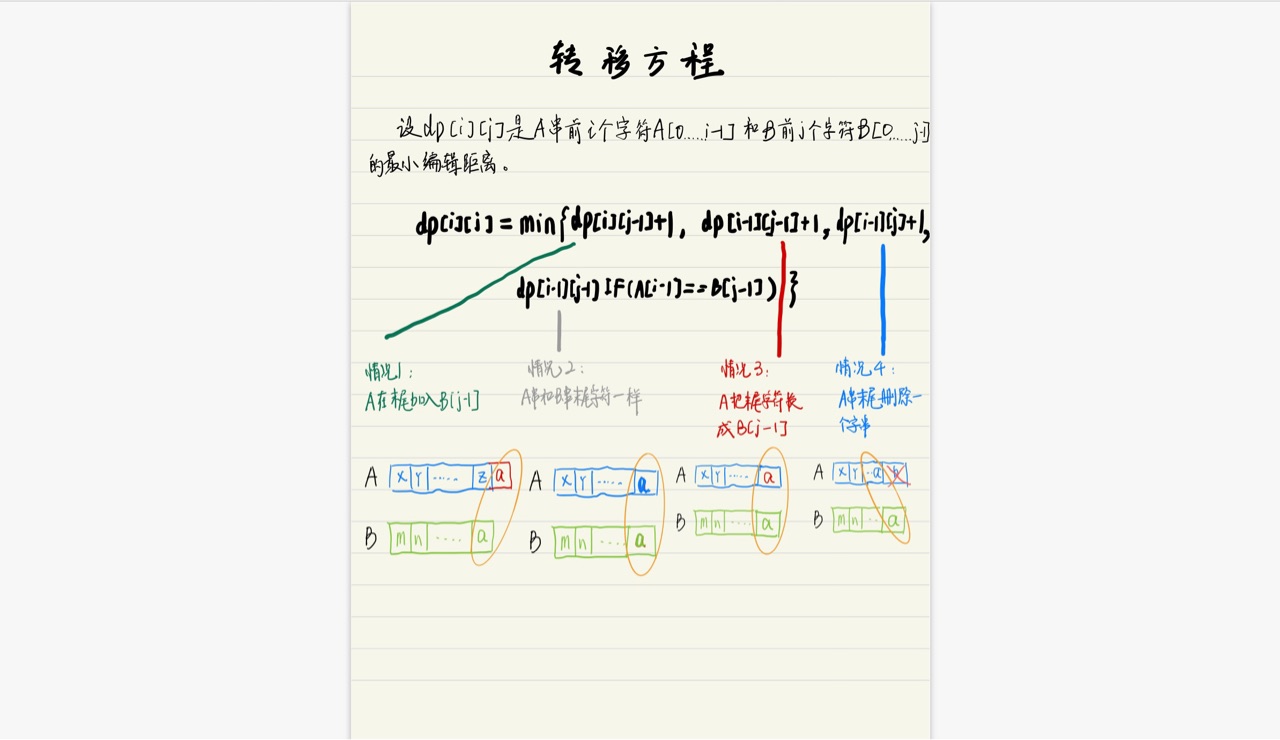
先考虑最后一步，那至少必须是A[m - 1] == B[n - 1], 要达到这个目的，分成4种情况:
1. 在A串末尾插入一个字符，字符=B串最后一个字符B[n - 1]
2. A串和B串末尾字符本身就一样
3. A串末尾字符换成B[n - 1]这个字符
4. A串末尾删除一个字符

Java 代码

class Solution {

    public int minDistance(String a, String b) {

        int m = a.length();
        int n = b.length();

        // 表示a的前i个字符和b的前j个字符最小的编辑距离
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                dp[i][j] = 0x3f3f3f3f;
                if (i == 0) {
                    dp[i][j] = j;
                    continue;
                }
                if (j == 0) {
                    dp[i][j] = i;
                    continue;
                }

                dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
                if (a.charAt(i - 1) == b.charAt(j - 1)) {
                    dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1]);
                }
            }
        }

        return dp[m][n];
    }
}