题目描述

给你一个房屋数组 houses 和一个整数 k ，其中 houses[i] 是第 i 栋房子在一条街上的位置，现需要在这条街上安排 k 个邮筒。

请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。

答案保证在 32 位有符号整数范围以内。

样例1

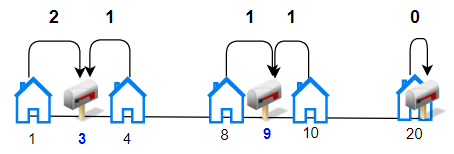
输入：houses = [1,4,8,10,20], k = 3
输出：5
解释：将邮筒分别安放在位置 3， 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。

样例2

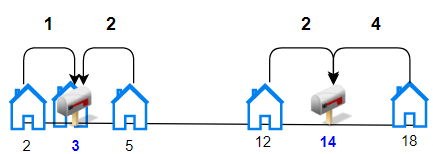
输入：houses = [2,3,5,12,18], k = 2
输出：9
解释：将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。

样例3

输入：houses = [7,4,6,1], k = 1
输出：8
示例 4：

样例4

输入：houses = [3,6,14,10], k = 4
输出：0

限制

• n == houses.length
• 1 <= n <= 100
• 1 <= houses[i] <= 10^4
• 1 <= k <= n
• 数组 houses 中的整数互不相同。

算法

(贪心 + 动态规划) $O(n² · m)$

1. 枚举所有邮箱放的位置会有达到 $C_{n}^{k}$ 种结果。所以我们采取另一种策略，先找出所有房子的势力范围，在势力范围内再定位邮箱放的位置。
2. 
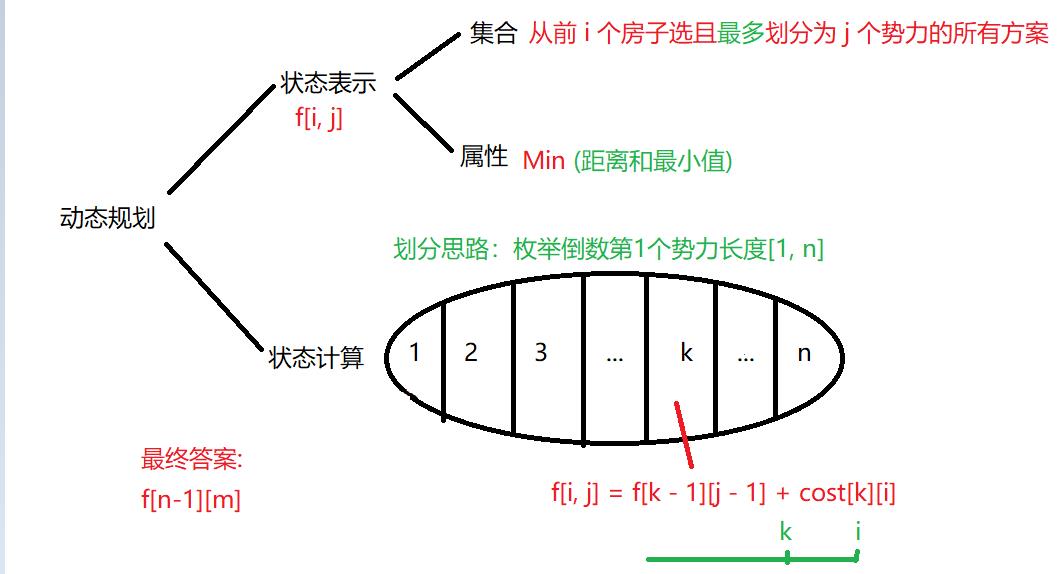
3. 分析思路:
   • 当只有 1 个邮箱的时候，邮箱放在放在所有房子的正中间会使得所有房子到邮箱的距离最短；
   • 当有 2 个邮箱的时候，邮箱会放在某 2 个区间内 [0, x] 和 [x+1, n], 其中 0 < x < n。 因此这 2 个邮箱会分别放在[0, x]的正中间位置 和 [x+1, n] 的正中间位置上，使得房子到邮箱的距离和最小。
   • 当有 k个邮箱的时候，我们就可以将所有房子划分成k个区间（相当于划分为k个势力范围），每个区间求出最短距离和相加，就能求出k个邮箱与所有房子的最短距离和
4. 分析初始化:
   • 由于最终答案要求的是min, 首先初始化全部为无穷大，像 MAX_INF、0x3f3f3f3f等等。
   • 表示的无穷大还可以更精细一些，根据题目给的数据范围，房子数量最多是1e4, 那任意2个房子中放1个邮箱的最大距离和是1e4, 最多是100个邮箱，所以这个无穷大可以是1e4 * 100=1e6来表示
   • 然后考虑，对f[0][i] 和 f[i][0]进行初始化
     • f[0][i] 表示只有1个房子且最多i个势力范围，自然是将邮箱就放在房子的位置距离最小为0;
     • f[i][0] 表示有i个房子且0个势力范围，这是无解的情况，初始化为无穷大来表示无解；
   • 初学者可能不知道接着要做什么:
     • 因为我们已经对边界f[0][i]、f[i][0]初始化好了，所以dp过程要从1开始，而不是从0开始
     • 初始化不一定非要写在dp过程外面，也可以写在dp过程里面的，只要能满足效果代码可以自由发挥~
5. 为什么状态表示的第二维要定义是 最多 j个势力范围？
   • 一开始状态表示可以随便想一个 至少、恰好、最多，看看能不能做出来，如果做不出来再换一个，毕竟就这三个，如何写这三类的初始化在提高课AcWing 1020. 潜水员有具体讲解；
   • 其实邮箱提供得越多，房子到邮箱距离和会更小：当有n个房子和n个邮箱，每个房子各一个邮箱，这样距离和就是0了，所以最终答案f[n-1][k] 就是题目所求。
   • 下面会给出 最多、恰好为j个势力范围的代码hh
   • 另外我也小结了这三种的初始化

时间复杂度

• 状态数是二维状态 f[i, j] $O(n · m)$
• 状态计算需要的时间是 $O(n)$
• 故总的时间复杂度是 $O(n² · m)$

空间复杂度

• 二维状态 f[i, j] 需要额外的空间是 $O(n · m)$
• 预处理所有[i, j]区间的距离和，需要额外的空间是 $O(n²)$
• 故总的空间复杂度是 $O(n · m) + O(n²)$

其他

• 最短距离和(绝对值不等式)，可以看看这题AcWing 104. 货仓选址

Go 代码1

• f[i, j]的集合表示：从前i个房子里选，且能放置最多 j个邮箱的最小距离和的所有方案

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

func minDistance(hs []int, m int) int {
    sort.Ints(hs[:])
    n := len(hs)

    const INF int = 1e6 + 10 // 1e4 * 100 = 1e6

    f := make([][]int, n)
    for i := 0; i < n; i ++ {
        f[i] = make([]int, m + 1)
    }

    cost := make([][]int, n)
    for i := 0; i < n; i ++ {
        cost[i] = make([]int, n)
    }

    for i := 0; i < n; i ++ {
        for j := i; j < n; j ++ {
            for k := i; k <= j; k ++ {
                cost[i][j] += abs(hs[k] - hs[i + (j - i + 1) / 2])
            }
        }
    }

    // 从前i个房子选且势力划分最多为j的最小距离和
    for i := 0; i < n; i ++ {
        f[i][0] = INF
    }

    // f[0][i] = 0, 只有1个房子不管多少势力, 距离和是0

    // 倒数第1个房子的势力是[1~k] 来划分
    for i := 1; i < n; i ++ {
        for j := 1; j <= m; j ++ {
            f[i][j] = INF
            for k := 0; k <= i; k ++ {
                t := 0
                if k > 0 {
                    t = f[k - 1][j - 1]
                }
                f[i][j] = min(f[i][j], t + cost[k][i])
            }
        }
    }

    return f[n - 1][m]
}

Go 代码2

• f[i, j]的集合表示：从前i个房子里选，且能放置恰好 j个邮箱的最小距离和的所有方案
• 和代码1唯一不同的是f[i, j]初始化的代码

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

func minDistance(hs []int, m int) int {
    sort.Ints(hs[:])
    n := len(hs)

    const INF int = 1e6 + 10 // 1e4 * 100 = 1e6

    f := make([][]int, n)
    for i := 0; i < n; i ++ {
        f[i] = make([]int, m + 1)
    }

    cost := make([][]int, n)
    for i := 0; i < n; i ++ {
        cost[i] = make([]int, n)
    }

    for i := 0; i < n; i ++ {
        for j := i; j < n; j ++ {
            for k := i; k <= j; k ++ {
                cost[i][j] += abs(hs[k] - hs[i + (j - i + 1) / 2])
            }
        }
    }

    // （初始化）从前i个房子选且势力划分恰好为j的最小距离和
    for i := 0; i < n; i ++ {
        for j := 0; j <= m; j ++ {
            f[i][j] = INF
        }
    }
    f[0][1] = 0

    // 倒数第1个房子的势力是[1~k] 来划分
    for i := 1; i < n; i ++ {
        for j := 1; j <= m; j ++ {
            for k := 0; k <= i; k ++ {
                t := 0
                if k > 0 {
                    t = f[k - 1][j - 1]
                }
                f[i][j] = min(f[i][j], t + cost[k][i])
            }
        }
    }

    return f[n - 1][m]
}