题目描述

We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with speed 1 unit per second. Some of the ants move to the left, the other move to the right.

When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions doesn’t take any additional time.

When an ant reaches one end of the plank at a time t, it falls out of the plank imediately.

Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right. Return the moment when the last ant(s) fall out of the plank.

样例

Example 1:

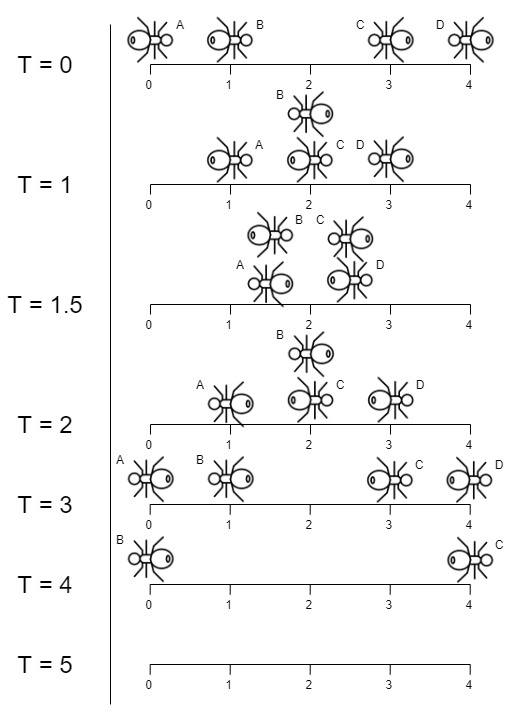
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
Note that the last moment when an ant was on the plank is t = 4 second, after that it falls imediately out of the plank. (i.e. We can say that at t = 4.0000000001, there is no ants on the plank).

Example 2:

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.

Example 3:

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.

Example 4:

Input: n = 9, left = [5], right = [4]
Output: 5
Explanation: At t = 1 second, both ants will be at the same intial position but with different direction.

Example 5:

Input: n = 6, left = [6], right = [0]
Output: 6

Constraints:

• 1 <= n <= 10^4
• 0 <= left.length <= n + 1
• 0 <= left[i] <= n
• 0 <= right.length <= n + 1
• 0 <= right[i] <= n
• 1 <= left.length + right.length <= n + 1
• All values of left and right are unique, and each value can appear only in one of the two arrays.

算法

(思维题) $O(n)$

这道题实际上就是《挑战程序设计竞赛》1.6轻松热身的例题，POJ-1852 Ants。蚂蚁碰撞后朝各自的反向向走，等效的结果是两只蚂蚁错开，不改变方向继续走。相比于POJ的题目，本题属于简化形式，给出了left和right，明确了每只蚂蚁的初始行走方向，那么初始向右走的蚂蚁，最后掉落的为距离右端点最远的蚂蚁，也就是n - min(right)；初始向左走的蚂蚁，最后掉落的为距离左端点最远的蚂蚁，也就是max(left)。

只需遍历一遍left和right数组，时间复杂度$O(n)$。

C++ 代码

class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        int maxVal = 0;
        for (auto & e : left) maxVal = max(maxVal, e);
        for (auto & e : right) maxVal = max(maxVal, n - e);

        return maxVal;
    }
};

还可以写成一行：

class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        return max(0, max(
            left.size() == 0 ? 0 : *max_element(left.begin(), left.end()), 
            right.size() == 0 ? 0 : n - *min_element(right.begin(), right.end())
        ));
    }
};