题目描述

Given a string num representing the digits of a very large integer and an integer k.

You are allowed to swap any two adjacent digits of the integer at most k times.

Return the minimum integer you can obtain also as a string.

样例

Example 1:

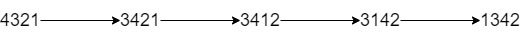
Input: num = "4321", k = 4
Output: "1342"
Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.

Example 2:

Input: num = "100", k = 1
Output: "010"
Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.

Example 3:

Input: num = "36789", k = 1000
Output: "36789"
Explanation: We can keep the number without any swaps.

Example 4:

Input: num = "22", k = 22
Output: "22"

Example 5:

Input: num = "9438957234785635408", k = 23
Output: "0345989723478563548"

Constraints:

• 1 <= num.length <= 30000
• num contains digits only and doesn’t have leading zeros.
• 1 <= k <= 10^9

一般涉及由数字组成的字符串，经过一系列操作让其最大/最小，往往涉及两个主题：贪心和逆序对。比如本题，洛谷 P1106 删数问题和洛谷P1323 删数问题。

本题最好想的思路是从贪心角度来思考，为了让最后的数字最小，那么肯定是数字越小，位置应该越靠前。从字符串的首部开始遍历，标记为left，每次找从left + 1到right的最小值，假设最小值的位置是pos，就需要将left到pos - 1的元素整体后移一个位置，将pos的元素移到left。

flag用来标记是否发生了数字交换（有点冒泡排序的意思），如果没有发生交换，并且已经到了字符串的末尾，就可以退出循环。时间复杂度$O(n^2)$，从数据范围推断，按理来说过不了。

这题的数据很迷，写了一个归并排序来计算逆序对的个数，其实就是冒泡排序交换的次数，如果k超过了cnt，直接排序返回即可。这种方法能过是计算cnt排除掉了最耗时的倒数两个测试数据，比赛时侥幸过关。这种思路对应解法一。

那么可以从上面思路的反方向考虑，因为字符串num里面的数字只能是0-9这十个数字中的一个，类似于分桶的思想，每个桶用队列来维护，总共十个桶，存储对应数字在num里出现的下标，显然每个桶里的下标值都是单调上升的。

现在假如k趋于无穷大，以num = "43031"为例，类似于分桶的思想，构建十个桶，每个桶用队列维护，存储对应数字的下标，显然每个桶（队列）里的（从队首看向队尾）下标是单调上升的。

已经假设k是无穷大，那么构建最小数的方法是：从所有非空桶里面选择最小的桶号（意味着每次选择了num里能够选择的最小数字），这个最小的数字放在位数越高的位置，显然得到数字会越小。也就是第一次我们取出了下标2，对应num里的0，此时他前面还没有数字被选择，肯定放在最高位最好，那么交换后num变成04331。

因为下标2对应的数字已经被使用过了，我们用一个数组used来记录下标对应的数字是否被使用过了，初始为0，被使用了标记为1。继续上面的思路，接下来该选择桶1里面的4，对应num里的1，此时最高位已经被占据了，他只能占据第二高的位置，变换后num为01433。

上面是假设k趋于无穷大，但是显然k是有限的，这意味着上面忽略了交换的代价。现在考虑存在交换代价时产生的影响。现在假设k = 1，num不变，此时如果最先选择下标2，它交换到最高位的代价是2，很显然是不满足条件的，接下来考虑下标4，也不满足。考虑下标1，它交换到最高位的代价是1，恰好满足。

此时规律不太明显，现在设k = 5，按照上面的思路，第一次将下标2对应的0换到最高位，代价为2；第二次将下标4对应的1换到第二高的位置，代价是3，现在考虑这个代价3是怎么得到的。在交换之前，used数组是：

在移动前，我们可以把当前位置的前面的结构描述成：

[A] [B] [curPos]
curPos：当前需要被移动的位置
[A]里面的数字都被是从某个位置移动过来的，并且都小于curPos对应的数字
[B]里面包含的是介于curPos和[A]之间没有被移动的数字

那么curPos移动到合适位置的代价就是移动到[B]里面的最高位，恰好就是curPos减去[A]的长度，此时used数组派上用场，计算[A]的长度，其实就是从0到curPos之间被使用过的位置的数量。

这样问题的主要矛盾在于如何解决一个数字使用后标记为1（单点修改），计算区间内的总和（查询区间和）。所以只要能解决前面两个矛盾的方法都可以采用，于是有线段树，树状数组，数列分块，依次对应第2，3，4种解法。

解法一：贪心 + 归并排序

时间复杂度$O(n^2)$，实际运行速度竟然还不错……

class Solution {
    string help;
    int cnt;
    int n;
    string s;
public:
    string minInteger(string num, int k) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        cnt = 0;
        n = num.size();
        calculate(num);

        if (cnt <= k) {
            sort(num.begin(), num.end());
            return num;
        }

        int left = 0, right, pos;
        bool flag = false;

        if (k >= n - 1) right = n - 1;
        else right = k;

        while (k) {
            flag = false;
            pos = left;
            for (int i = left; i <= right; ++i) {
                if (num[pos] > num[i]) pos = i;
            }

            for (int i = pos; i > left; --i) {
                std::swap(num[i], num[i - 1]);
                --k;
                flag = true;
            }

            if (!flag && left == n - 1) break;

            ++left;

            if (left + k < n - 1) right = left + k;
        }

        return num;
    }

    void calculate(string & num)
    {
        s = help = num; 
        mergeSort(0, n - 1);
    }

    void mergeSort(int left, int right)
    {
        if (left < right) {
            int mid = left + ((right - left) >> 1);
            mergeSort(left, mid);
            mergeSort(mid + 1, right);
            merge(left, mid + 1, right);
        }
    }

    void merge(int leftPos, int rightPos, int rightEnd)
    {
        int num = rightEnd - leftPos + 1; //需要归并的元素的数量
        int leftEnd = rightPos - 1; //前半部分的最右端的下标
        int tmp = leftPos;

        while (leftPos <= leftEnd && rightPos <= rightEnd) {
            if (s[leftPos] <= s[rightPos]) {
                help[tmp++] = s[leftPos++];
            }
            else {
                cnt += leftEnd - leftPos + 1;
                help[tmp++] = s[rightPos++];
            }
        }

        while (leftPos <= leftEnd) {
            help[tmp++] = s[leftPos++];
        }

        while (rightPos <= rightEnd) {
            help[tmp++] = s[rightPos++];
        }

        for (int i = 0; i < num; ++i) {
            s[rightEnd] = help[rightEnd];
            --rightEnd;
        }
    }
};

解法二：线段树

构建带延迟标记的线段树，来实现单点修改和查询区间和。每次查询和修改都是$O(\log n)$，时间复杂度$O(n \log n)$。关于线段树的解释可以参见《算法竞赛进阶指南》0x43部分。

class Solution {
    struct SegmentTree
    {
        int left, right;
        long long sum, lazy;

        //SegmentTree(): left(0), right(0), sum(0), lazy(0) {}
    };

    vector<SegmentTree> tree;
    int n;

    #define left(x) tree[x].left
    #define right(x) tree[x].right
    #define sum(x) tree[x].sum
    #define lazy(x) tree[x].lazy

    inline int leftChild(int x) { return x << 1; }
    inline int rightChild(int x) { return x << 1 | 1; }
    inline int length(int x) { return right(x) - left(x) + 1; }

    inline void update(int root)
    {
        sum(root) = sum(leftChild(root)) + sum(rightChild(root));
    }

    void build(int root, int l, int r)
    {
        left(root) = l;
        right(root) = r;

        if (l == r) { sum(root) = 0; return; }

        int mid = l + ((r - l) >> 1);
        build(leftChild(root), l, mid);
        build(rightChild(root), mid + 1, r);

        update(root);
    }

    void pushDown(int root)
    {
        if (lazy(root)) {
            sum(leftChild(root)) += lazy(root) * length(leftChild(root));
            sum(rightChild(root)) += lazy(root) * length(rightChild(root));

            lazy(leftChild(root)) += lazy(root);
            lazy(rightChild(root)) += lazy(root);
            lazy(root) = 0;
        }
    }

    void change(int root, int pos, long long val)
    {
        if (left(root) == right(root)) { sum(root) = val; return; }

        int mid = left(root) + ((right(root) - left(root)) >> 1);

        if (pos <= mid) change(leftChild(root), pos, val);
        else change(rightChild(root), pos, val);

        update(root);
    }

    long long query(int root, int l, int r)
    {
        if (left(root) == l && right(root) == r) return sum(root);

        pushDown(root); //延迟标记下传

        int mid = left(root) + ((right(root) - left(root)) >> 1);
        if (r <= mid) return query(leftChild(root), l, r);
        else if (l > mid) return query(rightChild(root), l, r);

        return query(leftChild(root), l, mid) + query(rightChild(root), mid + 1, r);
    }

public:
    string minInteger(string num, int k) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        n = num.size();
        string res;
        tree.resize((n + 5) * 4);
        build(1, 1, n);

        vector<queue<int>> digit(10);
        for (int i = 0; i < n; ++i) digit[num[i] - '0'].push(i);

        while (res.size() < n) {
            for (int i = 0; i < 10; ++i) {
                if (digit[i].empty()) continue;

                int curPos = digit[i].front(); 
                int cost = curPos - query(1, 1, curPos + 1);
                if (cost <= k) {
                    k -= cost;
                    res.push_back('0' + i);
                    digit[i].pop();
                    change(1, curPos + 1, 1);
                    break;
                }
            }
        }

        return res;
    }
};

解法三：树状数组

涉及lowbit运算，可以参考《算法竞赛进阶指南》0x01位运算部分。树状数组可参考0x42部分。

每次查询和修改的时间复杂度$O(\log n)$，时间复杂度$O(n \log n)$。

class Solution {
    vector<int> preSum;
    int n;

    inline int lowbit(int x) { return x & (-x); }

    //查询[1, pos]内前缀和
    int query(int pos)
    {
        int res = 0;
        while (pos) {
            res += preSum[pos];
            pos -= lowbit(pos);
        }

        return res;
    }

    //修改位于pos位置的数值为val
    void change(int pos, int val)
    {
        while (pos <= n) {
            preSum[pos] += val;
            pos += lowbit(pos);
        }
    }

public:
    string minInteger(string num, int k) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        n = num.size();
        preSum.resize(n + 1, 0);

        vector<queue<int>> digit(10);
        for (int i = 0; i < n; ++i) digit[num[i] - '0'].push(i);

        string res;
        while (res.size() < n) {
            for (int i = 0; i < 10; ++i) {
                if (digit[i].empty()) continue;

                int curPos = digit[i].front(); 
                int cost = curPos - query(curPos + 1);
                if (cost <= k) {
                    k -= cost;
                    res.push_back('0' + i);
                    digit[i].pop();
                    change(curPos + 1, 1);
                    break;
                }
            }
        }

        return res;
    }
};

解法四：数列分块

其实就是hzwer数列分块九题里的区间加法，区间查询。单点修改可以看成长度为1的区间加法。

数列分块是将数组分成$\sqrt{n}$块，维护一个加法标记，同时维护每个块的和，完整的块进行标记，不完整的块直接暴力修改。查询和修改的时间复杂度是$O(\sqrt{n})$，时间复杂度$O(n \sqrt{n})$。

class Solution {
    vector<int> seq, sum, addTag, belong;
    int n, blockNum;

    void init()
    {
        seq.resize(n + 1, 0);
        sum.resize(n + 1, 0);
        belong.resize(n + 1);
        addTag.resize(n + 1);

        blockNum = sqrt(n);

        for (int i = 1; i <= n; ++i) belong[i] = (i - 1) / blockNum + 1;
    }

    //查询[left, right]内前缀和
    int query(int left, int right)
    {
        int res = 0;
        for (int i = left; i <= min(belong[left] * blockNum, right); ++i)
            res += seq[i] + addTag[belong[left]];

        if (belong[left] != belong[right]) {
            for (int i = (belong[right] - 1) * blockNum + 1; i <= right; ++i)
                res += seq[i] + addTag[belong[right]];
        }

        for (int i = belong[left] + 1; i <= belong[right] - 1; ++i)
            res += sum[i] + blockNum * addTag[i];

        return res;
    }

    //[left, right]的区间增加val
    void change(int left, int right, int val)
    {
        for (int i = left; i <= min(belong[left] * blockNum, right); ++i) {
            seq[i] += val;
            sum[belong[left]] += val;
        }

        if (belong[left] != belong[right]) {
            for (int i = (belong[right] - 1) * blockNum + 1; i <= right; ++i) {
                seq[i] += val;
                sum[belong[right]] += val;
            }
        }

        for (int i = belong[left] + 1; i <= belong[right] - 1; ++i) {
            addTag[i] += val;
        }
    }

public:
    string minInteger(string num, int k) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        n = num.size();
        init();

        vector<queue<int>> digit(10);
        for (int i = 0; i < n; ++i) digit[num[i] - '0'].push(i);

        string res;
        while (res.size() < n) {
            for (int i = 0; i < 10; ++i) {
                if (digit[i].empty()) continue;

                int curPos = digit[i].front(); 
                int cost = curPos - query(1, curPos + 1);
                if (cost <= k) {
                    k -= cost;
                    res.push_back('0' + i);
                    digit[i].pop();
                    change(curPos + 1, curPos + 1, 1);
                    break;
                }
            }
        }

        return res;
    }
};