题目描述

有一块木板，长度为 n 个 单位。一些蚂蚁在木板上移动，每只蚂蚁都以 每秒一个单位 的速度移动。其中，一部分蚂蚁向 左 移动，其他蚂蚁向 右 移动。

当两只向 不同 方向移动的蚂蚁在某个点相遇时，它们会同时改变移动方向并继续移动。假设更改方向不会花费任何额外时间。

而当蚂蚁在某一时刻 t 到达木板的一端时，它立即从木板上掉下来。

给你一个整数 n 和两个整数数组 left 以及 right。两个数组分别标识向左或者向右移动的蚂蚁在 t = 0 时的位置。请你返回最后一只蚂蚁从木板上掉下来的时刻。

样例

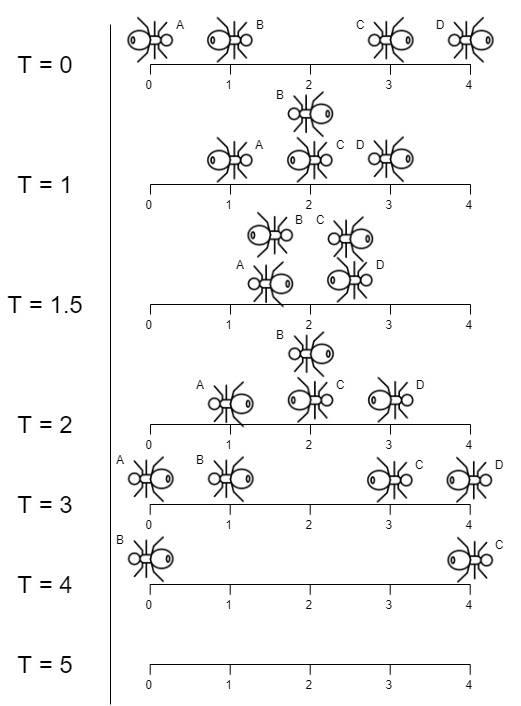
输入：n = 4, left = [4,3], right = [0,1]
输出：4
解释：如上图所示：
-下标 0 处的蚂蚁命名为 A 并向右移动。
-下标 1 处的蚂蚁命名为 B 并向右移动。
-下标 3 处的蚂蚁命名为 C 并向左移动。
-下标 4 处的蚂蚁命名为 D 并向左移动。
请注意，蚂蚁在木板上的最后时刻是 t = 4 秒，之后蚂蚁立即从木板上掉下来。
（也就是说在 t = 4.0000000001 时，木板上没有蚂蚁）。

输入：n = 7, left = [], right = [0,1,2,3,4,5,6,7]
输出：7
解释：所有蚂蚁都向右移动，下标为 0 的蚂蚁需要 7 秒才能从木板上掉落。

输入：n = 7, left = [0,1,2,3,4,5,6,7], right = []
输出：7
解释：所有蚂蚁都向左移动，下标为 7 的蚂蚁需要 7 秒才能从木板上掉落。

输入：n = 9, left = [5], right = [4]
输出：5
解释：t = 1 秒时，两只蚂蚁将回到初始位置，但移动方向与之前相反。

输入：n = 6, left = [6], right = [0]
输出：6

限制

• 1 <= n <= 10^4
• 0 <= left.length <= n + 1
• 0 <= left[i] <= n
• 0 <= right.length <= n + 1
• 0 <= right[i] <= n
• 1 <= left.length + right.length <= n + 1
• left 和 right 中的所有值都是唯一的，并且每个值 只能出现在二者之一 中。

算法

(模拟) $O(n)$

1. 两只蚂蚁相遇可以忽略，因为交换方向如果不考虑蚂蚁编号的话实际上等于没有交换。
2. 对于向左走的蚂蚁，需要的时间等于初始的位置；对于向右走的蚂蚁，需要的时间等于长度减去初始位置。

时间复杂度

• 分别遍历两个数组一次，时间复杂度为 $O(n)$。

空间复杂度

• 仅需要常数的额外空间。

C++ 代码

class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        int ans = 0;
        for (int x : left)
            ans = max(ans, x);

        for (int x : right)
            ans = max(ans, n - x);

        return ans;
    }
};