题目描述

给定一个字符串 num 和一个整数 k。其中，num 表示一个很大的整数，字符串中的每个字符依次对应整数上的各个 数位。

你可以交换这个整数相邻数位的数字 最多 k 次。

请你返回你能得到的最小整数，并以字符串形式返回。

样例

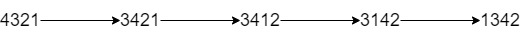
输入：num = "4321", k = 4
输出："1342"
解释：4321 通过 4 次交换相邻数位得到最小整数的步骤如上图所示。

输入：num = "100", k = 1
输出："010"
解释：输出可以包含前导 0 ，但输入保证不会有前导 0。

输入：num = "36789", k = 1000
输出："36789"
解释：不需要做任何交换。

输入：num = "22", k = 22
输出："22"

输入：num = "9438957234785635408", k = 23
输出："0345989723478563548"

限制

• 1 <= num.length <= 30000
• num 只包含 数字 且不含有 前导 0。
• 1 <= k <= 10^9

算法

(贪心，树状数组) $O(n \log n)$

1. 贪心的规则是每次尽可能的取一个小的数字放到最前。
2. 首先将每个数字的位置存放在一个队列中。
3. 从最高位开始填数字，从小到大枚举数字，并计算填当前数字所需要的最少步数。
4. 最小步数等于数字的原下标减去偏移量，其中偏移量为原下标小于该数字下标，且被使用过的数字的个数。
5. 偏移量的计算可以通过树状数组来解决，树状数组维护前缀和，如果使用了当前数字，就在当前数字的下标上累加 1。查询时，直接查询当前下标的前缀和。
6. 注意，代码中树状数组的下标是从 1 开始的。

时间复杂度

• 每个位置最多需要枚举 10 次，枚举的每次需要查询或更新树状数组。
• 故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储每个数字的下标队列和树状数组。

C++ 代码

class Solution {
private:
    vector<int> f;

    void update(int x, int n, int y) {
        for (; x <= n; x += x & -x)
            f[x] += y;
    }

    int query(int x) {
        int tot = 0;
        for (; x; x -= x & -x)
            tot += f[x];

        return tot;
    }

public:
    string minInteger(string num, int k) {
        int n = num.size();
        vector<queue<int>> v(10);

        for (int i = 0; i < n; i++)
            v[num[i] - '0'].push(i);

        f.resize(n + 1, 0);

        for (int i = 0; i < n; i++)
            for (int d = 0; d < 10; d++) {
                if (v[d].empty()) continue;
                int x = v[d].front();
                int offset = query(x + 1);

                if (x - offset <= k) {
                    num[i] = d + '0';
                    k -= x - offset;
                    update(x + 1, n, 1);

                    v[d].pop();
                    break;
                }
            }

        return num;
    }
};