题目描述

在一个 m x n 的网格上有一个球，给定球的起点坐标 (i, j)，你每次可以将这个球移动到四个方向（上下左右）相邻的格子上或者移出网格边界。然而，你最多可以移动 N 次。求出所有可以将球移出网格边界的路径数量。答案数可能很大，返回模 109+7109+7 后的结果。

样例

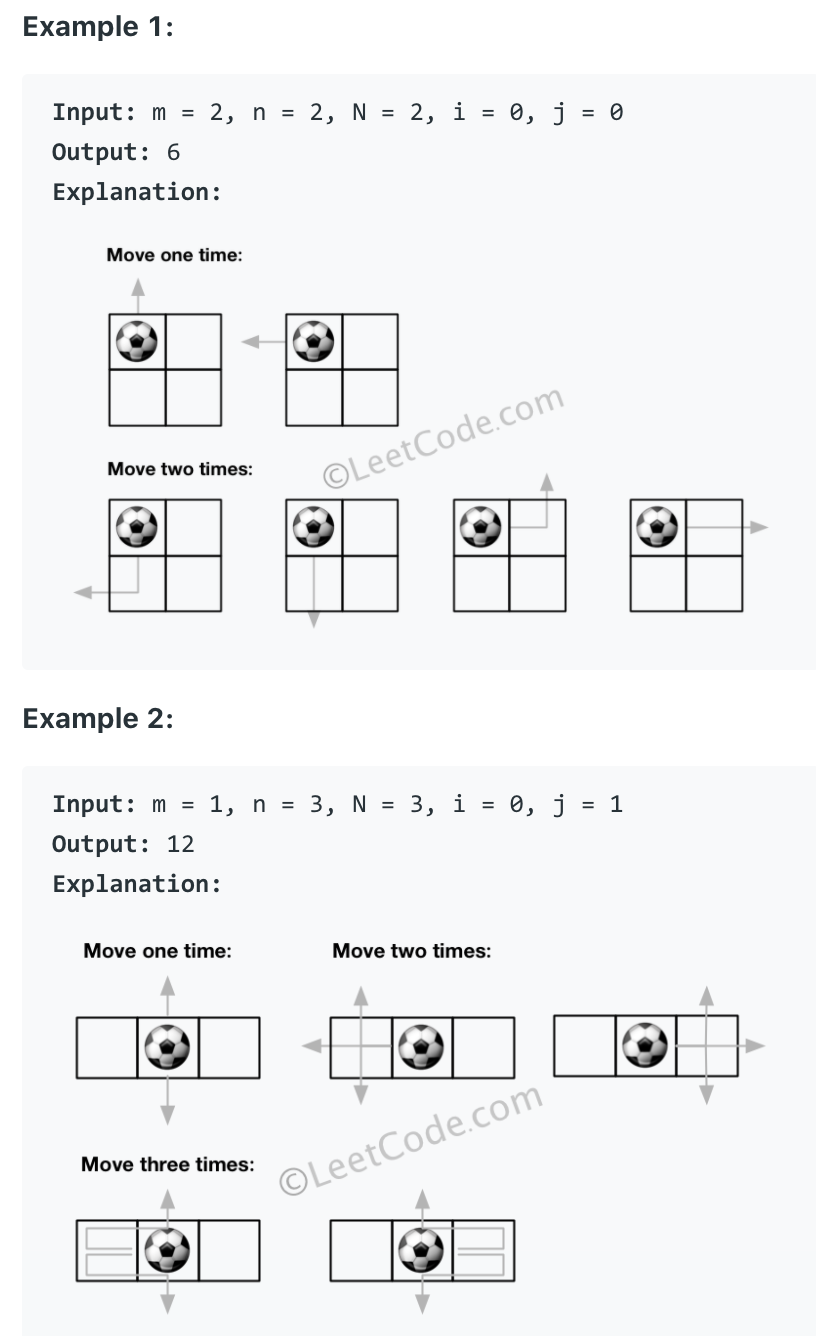
算法1

(动态规划) O(n^3)

1.从边界到出发点的逆向移动。令边界上的格子的初始值为1（起点），考虑经过N步之后，到达(i,j)的方案有多少。
dp[i,j,k] = dp[i-1,j,k-1] +  dp[i+1,j,k-1] + dp[i,j-1,k-1] + dp[i,j+1,k-1];

2.对于那些处在边界的格子，必须在每一步都赋值为1

Java 代码

class Solution {

    public int findPaths(int m, int n, int N, int i, int j) {
        // 从任意界外走N步到点[i,j]的方案总数
        int[][][] dp = new int[N + 1][m][n];
        for (int k = 1; k <= N; k++) {
            for (int x = 0; x < m; ++x) {
                for (int y = 0; y < n; ++y) {
                    long v1 = (x == 0) ? 1 : dp[k - 1][x - 1][y];
                    long v2 = (x == m - 1) ? 1 : dp[k - 1][x + 1][y];
                    long v3 = (y == 0) ? 1 : dp[k - 1][x][y - 1];
                    long v4 = (y == n - 1) ? 1 : dp[k - 1][x][y + 1];
                    dp[k][x][y] = (int) ((v1 + v2 + v3 + v4) % 1000000007);
                }
            }
        }

        return dp[N][i][j];
    }
}