本题所求为 最长公共上升子序列 由两个前导知识 最长上升子序列 和 最长公共子序列 组成

先放闫式DP思考图

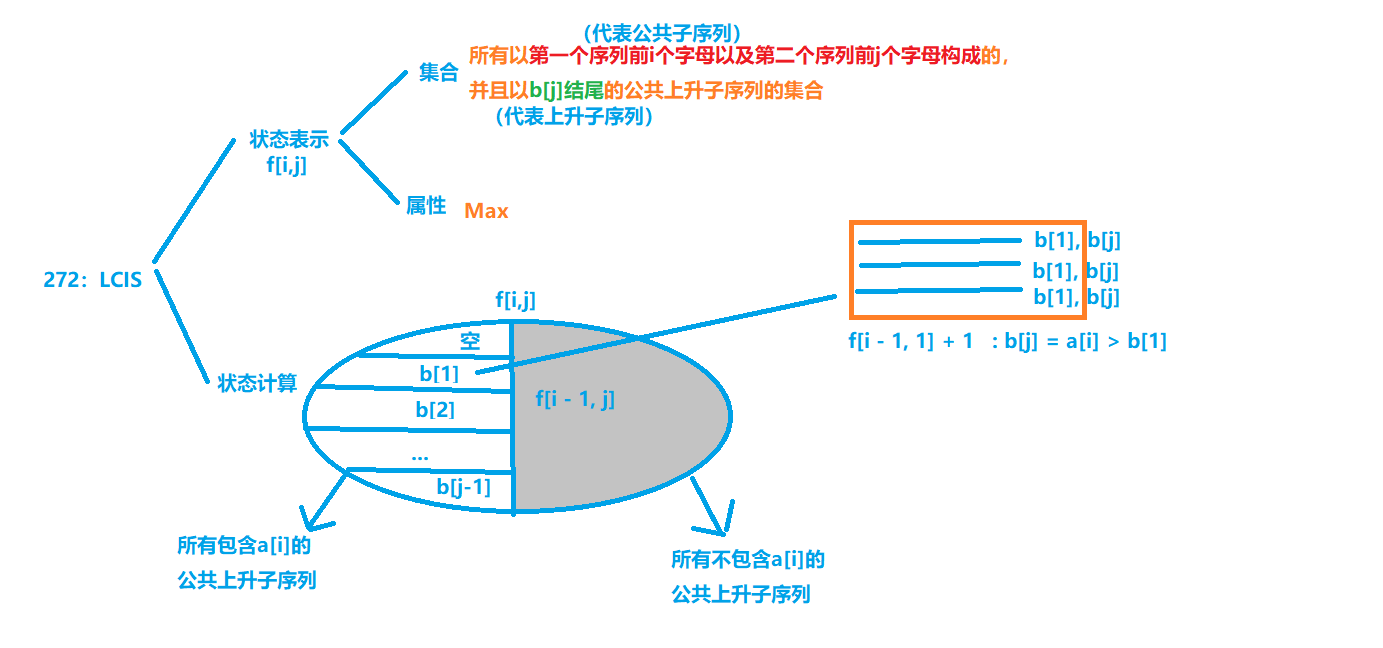
状态表示：
集合：f[i, j]表示第一个序列前i个字母以及第二个序列前j个字母，并且以b[j]结尾的公共上升子序列的集合
属性：代表f[i, j]这个集合子序列中长度最大值

（根据公共子序列中是否包含a[i]划分，实质就是a[i] == b[j]与否）
我们先通过a[i] == b[j]成立与否，划分为两部分
a[i] != b[j] –> 无法构成新的公共子序列，f[i][j] = f[i - 1][j]
a[i] == b[j] –> 可以构成新的公共子序列，将其继续进行划分
划分依据：公共子序列倒数第二个元素在b[]序列中所对应的数
子序列只包含b[j]本身 –> f[i][j] = max(f[i][j], 1)
子序列倒数第二个数是b[1] –> f[i][j] = max(f[i][j], f[i - 1][1] + 1)
…
子序列倒数第二个数是b[j - 1] –> f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1)
//若存在倒数第二个数，则有 b[j] > b[k] 方能构成上升子序列
//f[i][k]由于a[i] = b[j] != b[k]导致f[i][k] = f[i - 1][k]
//与此同时f[i][k] = f[i - 1][k] 所以虽使用f[i][j] = max(f[i][j], f[i][k] + 1)答案一致，但意义不同

直接实现上述思路代码

for (int i = 1; i <= n; ++ i)
        for (int j = 1; j <= n; ++ j) {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) {
                f[i][j] = max(f[i][j], 1);
                for (int k = 1; k < j; ++ k)
                    if (b[j] > b[k])
                        f[i][j] = max(f[i][j], f[i - 1][k] + 1);
            }
        }

可以发现a[i] == b[j]情况下if (b[j] > b[k])可等同于if (a[i] > b[k])，

for (int k = 1; k < j; ++ k)
    if (a[i] > b[k]) // b[j] > b[k]
        f[i][j] = max(f[i][j], f[i - 1][k] + 1);

所代表意义为求满足a[i] > b[k]情况下所有的f[i - 1][k] + 1的最大值,无需遍历k，可在前两个循环中求出
设g[i][j]来表示满足a[i] > b[j]的最长公共上升子序列长度加一 g[i][j] = max(g[i][j], f[i - 1][j] + 1)

for (int i = 1; i <= n; ++ i) {
        g[i][0] = 1;
        for (int j = 1; j <= n; ++ j) {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], g[i][j - 1]);
            g[i][j] = g[i][j - 1];
            if (a[i] > b[j]) g[i][j] = max(g[i][j], f[i - 1][j] + 1);
        }
}

可发现g[i][j]在第i行时随着j增大而呈现不下降性质，再进行优化

for (int i = 1; i <= n; ++ i) {
        int maxv = 1;
        for (int j = 1; j <= n; ++ j) {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
}

总代码如下

#include <bits/stdc++.h>

using namespace std;

const int N = 3005;

int n;
int a[N], b[N];
int f[N][N];
int g[N][N];  

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> a[i];
    for (int j = 1; j <= n; ++ j) cin >> b[j];


    for (int i = 1; i <= n; ++ i) {
        int maxv = 1;
        for (int j = 1; j <= n; ++ j) {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    int ans = 0;
    for (int i = 1; i <= n; ++ i) ans = max(f[n][i], ans);

    cout << ans << "\n";
    return 0;
}