题目描述

有两台机器 A，B 以及 K 个任务。

机器 A 有 N 种不同的模式（模式0~N-1），机器 B 有 M 种不同的模式（模式0~M-1）。

两台机器最开始都处于模式0。

每个任务既可以在A上执行，也可以在B上执行。

对于每个任务 i，给定两个整数 a[i] 和 b[i]，表示如果该任务在 A 上执行，需要设置模式为 a[i]，如果在 B 上执行，需要模式为 b[i]。

任务可以以任意顺序被执行，但每台机器转换一次模式就要重启一次。

求怎样分配任务并合理安排顺序，能使机器重启次数最少。

数据范围

$N,M<100,K<1000$
$0≤a[i]<N$
$0≤b[i]<M$

样例

输入
5 5 10
0 1 1
1 1 2
2 1 3
3 1 4
4 2 1
5 2 2
6 2 3
7 2 4
8 3 3
9 4 3
0

输出
3

算法1

二分图最小点覆盖 多组测试数据$O(n^2)$

对于每个任务来说，两个机器都可以完成，那么对于一个任务的两个模式方案a和b来说，可以在a和b之间连接一条边，那么所有的
任务构成一个二分图，题目说的最少重启次数也即找到最少的模式数量(点),使他们能覆盖所有的边。

模拟样例：

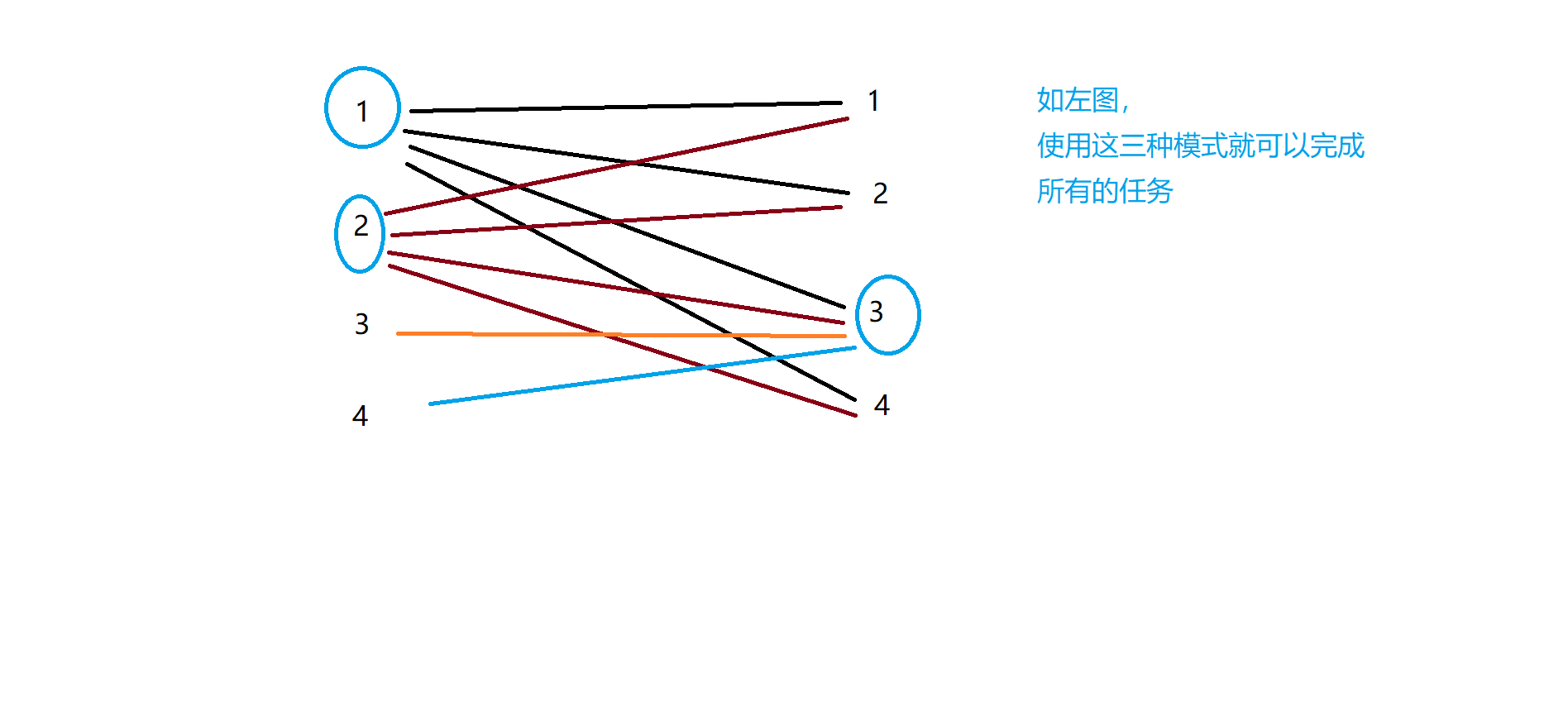
二分图的最小点覆盖等于二分图的最大匹配，证明见y总视频(逃ε=ε=ε=┏(゜ロ゜;)┛

C++ 代码

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int g[N][N];
bool st[N];
int mat[N];
int n,m,k;

bool find(int u){
    for(int i = 1; i<m; i++){
        if(!g[u][i] || st[i]) continue;
        int t = mat[i]; 
        st[i] = true;
        if(t == 0 || find(t)){
            mat[i] = u;
            return true;
        } 
    }
    return false;
}
int main()
{
    while(cin>>n,n){
        cin>>m>>k;

        memset(g,0,sizeof g);
        memset(mat,0,sizeof mat);
        while(k--){
            int a,b,c;
            cin>>c>>a>>b;
            if(a == 0 || b == 0) continue;  //机器一开始处于模式0，所以不用考虑
            g[a][b] = 1;
        }

        int res = 0;
        for(int i = 1; i<n; i++){
            memset(st,0,sizeof st);
            if(find(i)){
                res ++;
            }
        }
        cout<<res<<endl;
    }
}