题目如题

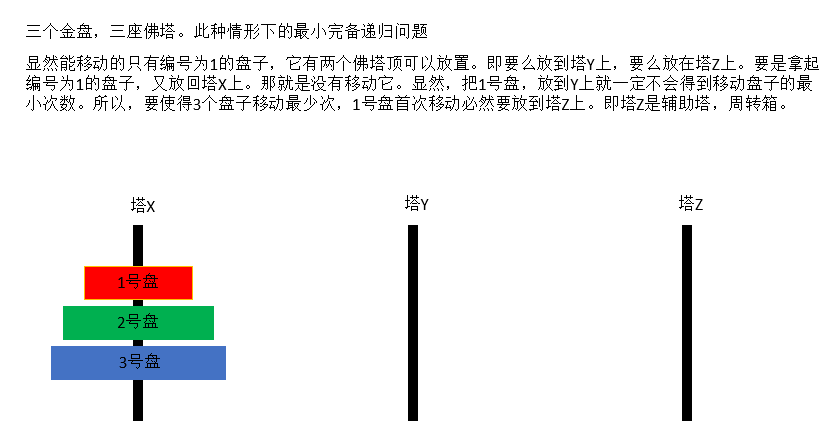
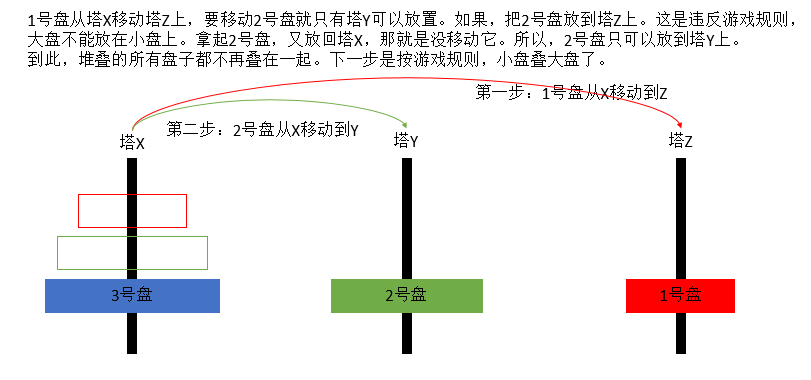
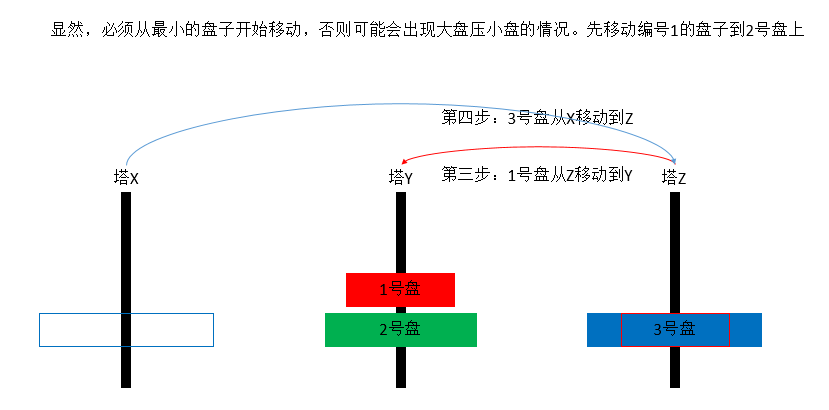
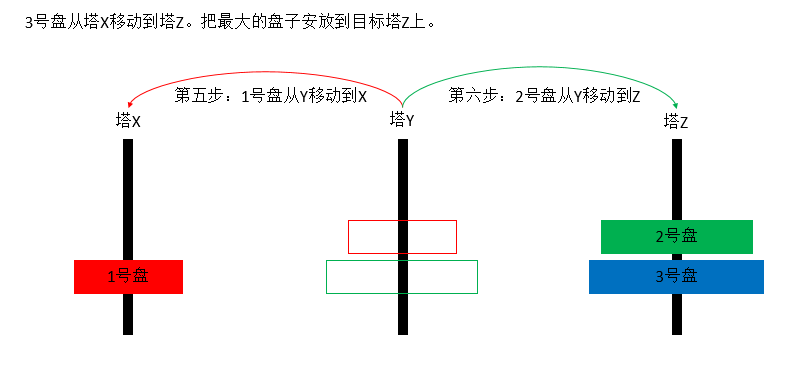
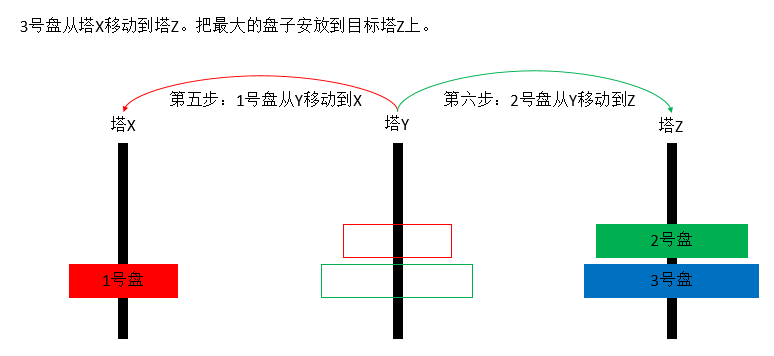
三个塔的情况下：把最下面的盘子上面的n – 1个盘子当做一个整体。最终目的是要把n – 1个盘子放到
Y塔上临时周转。不然，放到Z塔上就得不到最小次数的移动情况。假如n -  1个盘子移动到Y塔上用了a次
X塔上的最后一个最大的盘子可以直接从X移动到Z上。这是一次移动。把n - 1个盘子移动到Z塔又得用
a次移动才办得到。所以，最少的移动次数为：2 * a + 1 次移动。

四个塔就是先把X塔上的盘子分成两部分。前 i 个盘子和后n - i 个盘子。移动前 i 个盘子时，有4个塔可以
利用。因为，下面的第 n - i 个盘子比  i 个盘子中的任意一个都大。当前 i 个盘子放定以后。同样的原因
导致后n -  i 个盘子不能放到那 i 个盘子所在的塔上。所以，n - i 个盘子的移动只有三个塔可以利用了。
显然，下面的 n - i 个盘子的移动最少次数是已经讨论过的三塔情况。假设，前面 i 个盘子的移动周转之用
的塔上 的最少次数为 b，那么一共最少移动次数为：2 * b + (2 * a + 1) 
即递推公式：f[n] = min{ 2 * f[ i ] + d[ n – i ] }  (  1 <=  i  < n  )

算法1 Y总的递推实现

C++ 代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 15, M = 12;  
int d[N], f[N];

int main() {
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    for(int i = 1; i <= M; i++) 
        d[i] = d[i - 1] * 2 + 1;

    for(int i = 1; i <= M; i++)
        for(int j = 0; j < i; j++)
            f[i] = min(f[i], f[j] * 2 + d[i - j]);
    for(int i = 1; i <= M; i++) cout << f[i] << endl;
    return 0;
} 

算法2 抄的网上的递归实现

C++ 代码

void move(int& s, char from, char to) {
    s++;
    cout << from << " -> " << to << endl;
}

void three(int u, int& s, char a, char b, char c) {
    if(u == 1) move(s, a, c);
    else{
        three(u - 1, s, a, c, b);
        move(s, a, c);
        three(u - 1, s, b, a, c);
    }
}

void four(int u, int& s, char a, char b, char c, char d) {
    if(u == 1) move(s, a, d);
    else {
        int k = u >> 1;
        four(u - k, s, a, c, d, b);
        three(k, s, a, c, d);
        four(u - k, s, b, a, c, d);
    }
}

// 开始盘子总数为奇数，输出是那么回事。总数是偶数的情况下，一声不吭。。。。
void five(int u, int& s, char a, char b, char c, char d, char e) {
    if(u == 1) move(s, a, e);
    else {
        int k = 0;
        if(u >> 1 & 1) k = u / 2 + 1;
        else k = u / 2;

        five(u - k, s, a, c, d, e, b);
        four(k, s, a, c, d, e);
        five(u - k, s, b, a, c, d, e);
    }
}

推广如何实现？